Interactive Chemical Reactivity Exploration

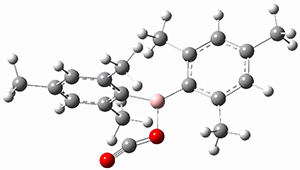
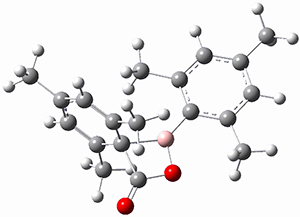
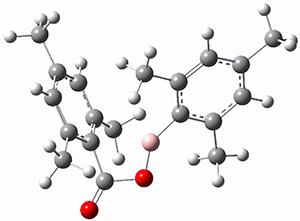
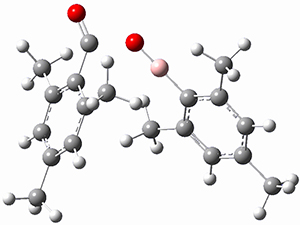
Moritz P. Haag, Alain C. Vaucher, Maël Bosson, Stéphane Redon, Markus Reiher ChemPhysChem 2014, 15, 3301 [arXiv]
Contributed by +Jan Jensen

"... it is still a major task to explore reaction mechanisms for molecular systems of even medium size (say, one to a few hundred atoms). ... The trial- and-error approach currently applied (guessing the important structures and refining them with local optimization methods) requires experience, luck, and time."

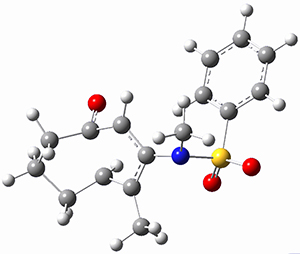
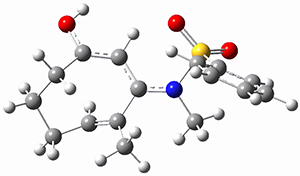
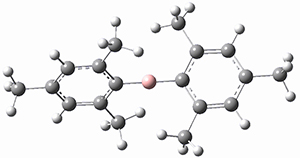
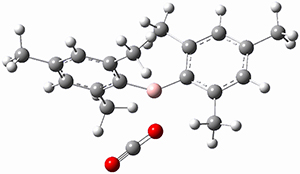
This paper provides a very innovative solution to this problem by interfacing a haptic device (a Phantom Desktop), the DFTB method, and the SAMSON visualization program to create a tool to interactively find intermediates and transition states.  

A haptic device is a force-feedback device that simulates a sense of touch based on computational data - in this case the forces on atoms computed by the DFTB method. This, in essence, allows you to provide physically force the reaction to occur. The premise is that this more intuitive approach to molecular modeling will make it easier for non-experts to quickly and thoroughly explore the reactivity of the system of interest. 

In order for this to work convincingly the computational method has to be fast enough to provide real-time feedback on the millisecond timescale and computers and approximate QM methods are now fast enough to provide this. As the user explores the potential energy surface key structures are automatically saved together with their energy and gradient.    

Applying this method leads to interesting practical challenges.  For example, the Phantom Desktop can only manipulate a single point, so many atomic degrees of freedom must be combined and some degree of automatic energy minimization must be included for most of the atoms. Then there is the "evasive adaption" of the system which naturally favors low energy structures, e.g. by moving atoms out of the way rather than reacting. 

I for one would very much like to get my hands on this setup and try this for myself.  Also, this really seems like an invaluable teaching tool! It seems like the many years of study required to build up a chemical intuition of reactivity could be replaced by a few weeks with this device!  Finally, there is the opportunity of citizen- or crowd sourced-science where non-scientists could help find novel reaction paths, much like fold.it for the protein folding problem.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands?

McKee, W. C.; Agarwal, J.; Schaefer, H. F.; Schleyer, P. v. R. Angew. Chem. Int. Ed. 2014, 53, 7875-7878
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Trying to get carbon to bond in unnatural ways seems to be a passion for many organic chemists! Schleyer has been interested in unusual carbon structures for decades and he and Schaefer now report a molecule with a pentacoordinate carbon bound to five other carbon atoms. Their proposed target is pentamethylmethane cation C(CH₃)₅⁺ 1.¹ The optimized geometry of 1, which has C_3h symmetry, at MP2/cc-pVTZ is shown in Figure 1. The bonds from the central carbon to the equatorial carbon are a rather long 1.612 Å, but the bonds to the axial carbon are even longer, namely 1.736 Å. Bader analysis shows five bond critical points, each connecting the central carbon to one of the methyl carbons. Wiberg bond index and MO analysis suggests that the central carbon is tetravalent, with a 2-electron-3-center bond involving the central and axial carbons.

1
TS1	TS2

Figure 1. MP2/cc-pVTZ optimized geometries of 1 and dissociation transition states.

So while 1 is a local energy minimum, it sits in a very shallow well. One computed dissociation path, which passes through TS1 (Figure 1) on its way to 2-methyl-butyl cation and methane has a barrier of only 1.65 kcal mol^-1 (CCSD(T)/CBS + ZPE). A second dissociation pathway goes through TS2 to t-butyl cation and ethane with a barrier of only 1.34 kcal mol^-1. Worse still is that the free energy estimates suggest “spontaneous dissociation … through both pathways”.

Undoubtedly, this will not be the last word on trying to torture a poor carbon atom.

References

(1) McKee, W. C.; Agarwal, J.; Schaefer, H. F.; Schleyer, P. v. R. "Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands?," Angew. Chem. Int. Ed. 2014, 53, 7875-7878, DOI: 10.1002/anie.201403314.

InChIs

1: InChI=1S/C6H15/c1-6(2,3,4)5/h1-5H3/q+1
InChIKey=GGCBGJZCTGZYFV-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Torquoselective Ring Opening of Fused Cyclobutenamides: Evidence for a Cis,Trans-Cyclooctadienone Intermediate

Wang, X.-N.; Krenske, E. H.; Johnston, R. C.; Houk, K. N.; Hsung, R. P.  J. Am. Chem. Soc. 2014, 136, 9802-9805
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Houk’s theory of torquoselectivity is a great achievement of computational chemistry, as told in Chapter 4.6 of the second edition of my book. Houk, in a collaboration with Krenske and Hsung, now report on an application of torquoselectivity in the formation of a cis-trans-cyclooctadienone intermediate.¹

The proposed reaction is shown in Scheme 1, where the bicyclic compound undergoes a conrotatory ring opening in just one orientation to form the E,E-cyclooctadienone, which can then ring close to product.

Scheme 1.

Houk ran M06-2x//6-311+G(d,p)//B3LYP/6-31G(d) computations on the model system 1, passing over the two torquodistinctive transition states TSEE and TSZZ, and on to produce the two cyclooctadienones2EE and 2ZZ, respectively. As seen in Figure 1, the barrier through TSEE is favored by 9.8 kcal mol^-1, and leads to the much more favorable cycloocatadienone 2EE.

1 0.0
TSEE 32.3	2EE 9.4
TSZZ 42.1	2ZZ 21.0
TS2 47.5

Figure 1. B3LYP/6-31G(d) optimized structures and relative free energies (kcal mol^-1) at M06-2x//6-311+G(d,p)//B3LYP/6-31G(d).

Ring closure taking TSEE to product goes through TS2 (Figure 1), with a very high barrier, 47.5 kcal mol^-1above reactant, suggesting that this path is not likely to occur. Instead, they propose that 2EE is first protonated (2EEH⁺) and then cyclizes through TS2H⁺ (Figure 2). This barrier is only 6.2 kcal mol^-1, some 44 kcal mol^-1 lower than the neutral process through TS2.

2EEH+

TS2H+

Figure 2. B3LYP/6-31G(d) optimized structures

References

(1) Wang, X.-N.; Krenske, E. H.; Johnston, R. C.; Houk, K. N.; Hsung, R. P. "Torquoselective Ring Opening of Fused Cyclobutenamides: Evidence for a Cis,Trans-Cyclooctadienone Intermediate," J. Am. Chem. Soc.2014, 136, 9802-9805, DOI: 10.1021/ja502252t.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Ionic materials and van der Waals

Bučko, Tomáš, Sébastien Lebègue, Jürgen Hafner, and János G. Ángyán. "Improved density dependent correction for the description of London dispersion forces." Journal of Chemical Theory and Computation 9, (2013): 4293-4299.

Bučko, Tomáš, Sébastien Lebègue, János G. Ángyán, and Jürgen Hafner. "Extending the applicability of the Tkatchenko-Scheffler dispersion correction via iterative Hirshfeld partitioning." The Journal of Chemical Physics 141, (2014): 034114.

Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission

One of the areas which has grown explosively in DFT in recent years is modelling van der Waals interactions (I’ve written about this before). The semi-empirical approach originated by Tkatchenko and Scheffler[1] (normally known as TS) uses the calculated DFT charge density, which is divided between the atoms in the system to give an effective volume occupied by each atom; the ratio of this volume to a free atom volume is then used to rescale the C6 coefficients and polarisabilities found for free atoms. This brings us to an ever-present problem with ab initio methods: how to divide a continuous charge density or wavefunction between the atoms in the system.

TS use Hirshfeld partitioning[2], which creates a distance-dependent weight for each atom according to the ratio between the free atom charge density for the atom and the sum of free atom charge densities for the whole system. This can be used to give a volume and hence the relevant vdW quantities (see Eq. 7-9 in [1] for more detail). But this is not the only way to divide space (and hence charge density) between atoms: Voronoi polyhedra, Bader’s atoms-in-molecules[3], and Becke’s integral partitioning[4] are only some of the methods in common use, along with Mulliken charges as a way of assigning charge to atoms. We discuss these methods in Section 17.2 of the book, and show an example of how different methods and basis sets can change the charge by more than half an electron.

The papers I want to discuss in this blog[5,6] address another problem with the Hirshfeld approach: as it uses free, neutral atoms as the references to divide the charge density, it performs poorly for ionic materials. Instead, they use an update of Hirshfeld partitioning which iterates the charge density decomposition, and interpolates between reference densities of the free atoms in different charge states. It is a relatively small change to make to the process, but has a very strong effect on ionic materials, improving agreement with experiment and high-level theory markedly[5].

Whenever a change is made to an approach, it is important to characterise the effect on the existing performance; in an extensive follow-up paper, the authors do this[6], looking at an large collection of test systems. The main criticism that can be made of the new, iterative approach is that it worsens the modelling of molecular interactions (particularly those which have an obvious van der Waals component). However, the improvement of other systems, particularly ionic solids and molecules interacting with charges on surfaces, is sufficiently strong that this would be well worth using in most circumstances. The authors make the parameters they have used clear (k point meshes, plane wave cutoffs), and the approach is available in VASP (though I would have preferred to have seen it made freely available!).

[1] Phys. Rev. Lett. 102, 073005 (2009) DOI:10.1103/PhysRevLett.102.073005
[2] Theor. Chim. Acta 44, 129 (1977) DOI:10.1007/BF00549096
[3] R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press (1990).
[4] J. Chem. Phys., 88, 2547 (1988) DOI:10.1063/1.454033
[5] J. Chem. Theory Comput. 9, 4293 (2013) DOI:10.1021/ct400694h
[6] J. Chem. Phys. 141, 034114 (2014) DOI:10.1063/1.4890003

Ultrafast X-ray Auger probing of photoexcited molecular dynamics

McFarland, B. K.; Farrell, J. P.; Miyabe, S.; Tarantelli, F.; Aguilar, A.; Berrah, N.; Bostedt, C.; Bozek, J. D.; Bucksbaum, P. H.; Castagna, J. C.; Coffee, R. N.; Cryan, J. P.; Fang, L.; Feifel, R.; Gaffney, K. J.; Glownia, J. M.; Martinez, T. J.; Mucke, M.; Murphy, B.; Natan, A.; Osipov, T.; Petrović, V. S.; Schorb, S.; Schultz, T.; Spector, L. S.; Swiggers, M.; Tenney, I.; Wang, S.; White, J. L.; White, W.; Gühr, M. Nat Commun 2014, 5, doi:10.1038/ncomms5235.
Highlighted by Mario Barbatti

The deconvolution of nuclear and electronic ultrafast motions poses a great challenge for spectroscopic approaches and nonadiabatic dynamics simulations has been a valuable tool to help with this task.

But are dynamics simulations providing reliable information?

Take, for instance, thymine. The ultrafast dynamics of this molecule has been under debate for a decade. 

Thymine has the longest excited-state lifetime among the five canonical nucleobases in the gas phase. According to Ref. (1), after 267-nm excitation, thymine shows a double-exponential deactivation with 105-fs and 5.12-ps time constants. 

The long time constant, which has been assigned to the excited-state lifetime of thymine, was attributed at first to a trapping of the population in the S₁ (nπ*) state after a quick relaxation from the initially excited S₂ (ππ*) state (2) (see Fig. 1). 

As a second possibility, an independent study proposed that the deactivation occurred solely on the ππ* state, without any major influence of the nπ* state (3). In this case, the trapping site would be located at another region of the S₁ surface at a minimum with ππ* character. 

Either way, from one of those S₁ minima, thymine would take a few picoseconds to find the seam of conical intersections to the ground state, explaining its longer lifetime. 

Fig. 1 - After photoexcitation, how does thymine returns to the ground state?

This interpretation has been disputed since different sets of dynamics simulations at CASSCF level predicted that the S₂ (ππ*) → S₁ (nπ*) relaxation time itself occurs on a few picoseconds (4,5). Hence both, elongated S₂ (ππ*) → S₁ (nπ*) relaxation and then S₁ (nπ*) trapping, would contribute to the long time constant.

This entangled story has gained another chapter with a curious twist (6): based on ultrafast X-ray Auger probe spectroscopy and simulations (ADC(2), CK-CIS), McFarland and co-authors found strong evidences that thymine excitation at 266 nm should populate the S₁ (nπ*) state within only 200 fs, just like in the first proposal.

It makes possible that the S₂ (ππ*) trapping was, after all, an artifact of dynamics simulations limited to CASSCF surfaces.

References

(1) Canuel, C.; Mons, M.; Piuzzi, F.; Tardivel, B.; Dimicoli, I.; Elhanine, M. J. Chem. Phys. 2005, 122, 074316-074316. doi:10.1063/1.1850469
(2) Perun, S.; Sobolewski, A. L.; Domcke, W. J. Phys. Chem. A 2006, 110, 13238-13244. doi:10.1021/jp0633897
(3) Merchán, M.; González-Luque, R.; Climent, T.; Serrano-Andrés, L.; Rodriuguez, E.; Reguero, M.; Pelaez, D. J. Phys. Chem. B 2006, 110, 26471-26476. doi:10.1021/jp066874a
(4) Hudock, H. R.; Levine, B. G.; Thompson, A. L.; Satzger, H.; Townsend, D.; Gador, N.; Ullrich, S.; Stolow, A.; Martínez, T. J. J. Phys. Chem. A 2007, 111, 8500-8508. doi:10.1021/jp0723665
(5) Szymczak, J. J.; Barbatti, M.; Soo Hoo, J. T.; Adkins, J. A.; Windus, T. L.; Nachtigallová, D.; Lischka, H. J. Phys. Chem. A 2009, 113, 12686-12693.doi:10.1021/jp905085x
(6) McFarland, B. K.; Farrell, J. P.; Miyabe, S.; Tarantelli, F.; Aguilar, A.; Berrah, N.; Bostedt, C.; Bozek, J. D.; Bucksbaum, P. H.; Castagna, J. C.; Coffee, R. N.; Cryan, J. P.; Fang, L.; Feifel, R.; Gaffney, K. J.; Glownia, J. M.; Martinez, T. J.; Mucke, M.; Murphy, B.; Natan, A.; Osipov, T.; Petrović, V. S.; Schorb, S.; Schultz, T.; Spector, L. S.; Swiggers, M.; Tenney, I.; Wang, S.; White, J. L.; White, W.; Gühr, M. Nat Commun 2014, 5, doi:10.1038/ncomms5235.

A two-coordinate boron cation featuring C–B+–C bonding

Shoji, Y.; Tanaka, N.; Mikami, K.; Uchiyama, M.; Fukushima, T.  Nat. Chem. 2014, 6, 498-503

Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This paper is a bit afield from the usual material I cover but this is an interesting reaction. Shoji and coworkers have prepared the two-coordinate boron species 1,¹ and confirmed its geometry by an x-ray crystal structure. What I find interesting is its reaction with CO₂, which gives 2 and organoboranes that are not identified, though presumably derived from 3.

M06-2x/6-311+G(d,p) computations support a hypothetical mechanism whereby first a complex between1 and CO₂ is formed (CP1), that is 4.4 kcal mol^-1 above isolated reactants. Then passing through TS1, which is 4.2 kcal mol^-1 above CP1, an intermediate is formed (INT), which is almost 6 kcal mol^-1 below starting materials. A second transition state is then traversed (about 1 kcal mol^-1 below starting materials), to form an exit complex between 2 and 3, which can then separate to the final products with an overall exothermicity of 10.6 kcal mol^-1. The structures of these critical points are shown in Figure 1.

1 (0.0)	CP1 (4.4)
TS1 (8.6)	INT (-5.7)
TS2 (-1.1)	CP2 (-9.0)

Figure 1. M06-2x/6-311+G(d,p) optimized structures. Relative energy in kcal mol^-1.

References

(1) Shoji, Y.; Tanaka, N.; Mikami, K.; Uchiyama, M.; Fukushima, T. "A two-coordinate boron cation featuring C–B⁺–C bonding," Nat. Chem. 2014, 6, 498-503, DOI: 10.1038/nchem.1948.

InChIs

1: InChI=1S/C18H22B/c1-11-7-13(3)17(14(4)8-11)19-18-15(5)9-12(2)10-16(18)6/h7-10H,1-6H3/q+1
InChIKey=WLUJABFTLHAEMI-UHFFFAOYSA-N

2: InChI=1S/C10H11O/c1-7-4-8(2)10(6-11)9(3)5-7/h4-5H,1-3H3/q+1
InChIKey=CUJVTHUIQVMVHD-UHFFFAOYSA-N

3: InChI=1S/C9H11BO/c1-6-4-7(2)9(10-11)8(3)5-6/h4-5H,1-3H3
InChIKey=ZJKBFARYTPYYGV-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.