Fokin, A. A.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Dahl, J. E. P.; Carlson, R. M. K.; Schreiner, P. R. J. Am. Chem. Soc., 2012, 134, 13641 (Paywall)
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
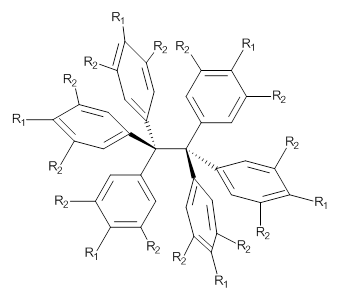
3: R1 = R2 = H
4: R1 = tBu, R2 = H
5: R1 = H, R2 = tBu
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
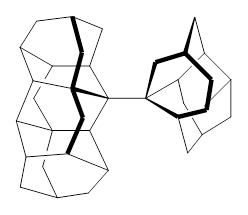
Schreiner has expanded on his previous paper1 regarding alkanes with very long C-C bonds, which I commented upon in this post. He and his colleagues report2 now a series of additional diamond-like and adamantane-like sterically congested alkanes that are stable despite have C-C bonds that are longer that 1.7 Å (such as 1! In addition they examine the structures and rotational barriers using a variety of density functionals.
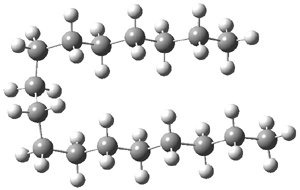
 1 | 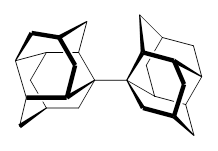 2 |
For 2, the experimental C-C distance is 1.647 Å. A variety of functionals all using the cc-pVDZ basis predict distances that are much too long: B3LYP, B96, B97D, and B3PW91. However, functionals that incorporate some dispersion, either through an explicit dispersion correction (Like B3LYP-D and B2PLYP-D) or with a functional that address mid-range or long range correlation (like M06-2x) or both (like ωB97X-D) all provide very good estimates of this distance.
On the other hand, prediction of the rotational barrier about the central C-C bond of 2 shows different functional performance. The experimental barrier, determined by 1H and 13C NMR is 16.0 ± 1.3 kcal mol-1. M06-2x, ωB97X-D and B3LYP-D, all of which predict the correct C-C distance, overestimate the barrier by 2.5 to 3.5 kcal mol-1, outside of the error range. The functionals that do the best in getting the rotational barrier include B96, B97D and PBE1PBE and B3PW91. Experiments and computations of the rotational barriers of the other sterically congested alkanes reveals some interesting dynamics, particularly that partial rotations are possible by crossing lower barrier and interconverting some conformers, but full rotation requires passage over some very high barriers.
In the closing portion of the paper, they discuss the possibility of very long “bonds”. For example, imagine a large diamond-like fragment. Remove a hydrogen atom from an interior position, forming a radical. Bring two of these radicals together, and their computed attraction is 27 kcal mol-1 despite a separation of the radical centers of more than 4 Å. Is this a “chemical bond”? What else might we want to call it?
A closely related chemical system was the subject of yet another paper3 by Schreiner (this time in collaboration with Grimme) on the hexaphenylethane problem. I missed this paper somehow near
the end of last year, but it is definitely worth taking a look at. (I should point out that this paper was already discussed in a post in the Computational Chemistry Highlights blog, a blog that acts as a journals overlay – and one I participate in as well.)
the end of last year, but it is definitely worth taking a look at. (I should point out that this paper was already discussed in a post in the Computational Chemistry Highlights blog, a blog that acts as a journals overlay – and one I participate in as well.)
So, the problem that Grimme and Schreiner3 address is the following: hexaphenylethane 3 is not stable, and 4 is also not stable. The standard argument for their instabilities has been that they are simply too sterically congested about the central C-C bond. However, 5 is stable and its crystal structure has been reported. The central C-C bond length is long: 1.67 Å. But why should 5 exist? It appears to be evenmore crowded that either 3 or 4. TPSS/TZV(2d,2p) computations on these three compounds indicate that separation into the two radical fragments is very exoergonic. However, when the “D3” dispersion correction is included, 3 and 4 remain unstable relative to their diradical fragments, but 5 is stable by 13.7 kcal mol-1. In fact, when the dispersion correction is left off of the t-butyl groups, 5 becomes unstable. This is a great example of a compound whose stability rests with dispersion attractions.

3: R1 = R2 = H
4: R1 = tBu, R2 = H
5: R1 = H, R2 = tBu
References
(1) Schreiner, P. R.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Schlecht, S.; Dahl, J. E. P.; Carlson, R. M. K.; Fokin, A. A. "Overcoming lability of extremely long alkane carbon-carbon bonds through dispersion forces," Nature 2011, 477, 308-311, DOI:10.1038/nature10367
(2) Fokin, A. A.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Dahl, J. E. P.; Carlson, R. M. K.; Schreiner, P. R. "Stable Alkanes Containing Very Long Carbon–Carbon Bonds," J. Am. Chem. Soc., 2012, 134, 13641-13650, DOI: 10.1021/ja302258q
(3) Grimme, S.; Schreiner, P. R. "Steric Crowding Can tabilize a Labile Molecule: Solving the Hexaphenylethane Riddle," Angew. Chem. Int. Ed., 2011, 50, 12639-12642, DOI:10.1002/anie.201103615