Computationally Augmented Retrosynthesis: Total Synthesis of Paspaline A and Emindole PB

Daria E. Kim, Joshua E. Zweig and Timothy R. Newhouse (2018)

Highlighted by Jan Jensen

Figure 2 from the paper reproduced under the CC-BY-NC-ND licence

This paper presents a rare example of using quantum chemical TS calculations to guide, rather than post-rationalise, organic synthesis. The authors wanted to design a retrosynthetic path that could be used to make two related natural products, paspaline A and emindole PB, that require either a ring closure (paspaline A) or a methyl shift (emindole PB). Three different routes were possible that lead to different functionalities that were relatively distant from the ring closure/methyl shift, which made it hard to predict the best route by chemical intuition.

Instead the authors used mPW1PW91/6-31+G(d,p)//B3LYP/6-31G(d) to find the TSs for both reactions for each of the three routes to predict the best route, which turns out to be "C". Route C did indeed work great in practice, while route A (predicted to be worst route) didn't give the desired results.

My guess is that the key here is that the synthetic question was reduced to a question of relative barrier heights of closely related reactions, i.e. ΔΔΔG^‡ = ΔΔG^‡(4→5) - ΔΔG^‡(4→6), which leads to maximum error cancellation. I hope this paper will lead to more use of QM to guide synthetic decisions and more work on making TS calculations even more accessible to synthetic chemists


This work is licensed under a Creative Commons Attribution 4.0 International License.

Electrocyclic reactions of cethrene derivatives

Šolomek, T.; Ravat, P.; Mou, Z.; Kertesz, M.; Juríček, M., "Cethrene: The Chameleon of Woodward–Hoffmann Rules." J. Org. Chem. 2018, 83, 4769-4774
Ravat, P.; Šolomek, T.; Häussinger, D.; Blacque, O.; Juríček, M., "Dimethylcethrene: A Chiroptical Diradicaloid Photoswitch." J. Am. Chem. Soc. 2018, 140, 10839-10847.
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Pericyclic reactions remain a fruitful area of research despite the seminal publication of the Woodward-Hoffmann rules decades ago. Here are two related papers of pericyclic reactions that violate the Woodward-Hoffmann rules.

First, Solomek, Ravat, Mou, Kertesz, and Jurícek reported on the thermal and photochemical electrocyclization reaction of diphenylcetherene 1a.¹ Though they were not able to directly detect the intermediate 2, through careful examination of the photochemical reaction, they were able to infer that the thermal cyclization goes via the formally forbidden conrotatory pathway (see Scheme 1).

Scheme 2.

Kinetic studies estimate the activation barrier is 14.1 kcal mol^-1. They performed DFT computations of the parent 1b using a variety of functionals with both restricted and unrestricted wavefunctions. The allowed pathway to 2syn is predicted to be greater than 27 kcal mol^-1, while the formally forbidden pathway to 2anti is estimated to have a lower barrier of about 23 kcal mol^-1. The two transition states for these different pathways are shown in Figure 1, and the sterics that force a helical structure to 1 help make the forbidden pathway more favorable.

TS(1b→2b-syn)

TS(1b→2b-anti)

Figure 1. (U)B3LYP/6-31G optimized geometries of the transition states taking 1 into 2.

Nonetheless, all of the DFT computations significantly overestimate the activation barrier. The authors make the case that a low-lying singlet excited state results in an early conical intersection that reduces the symmetry from C₂ to C₁. In this lower symmetry pathway, all of the states can mix, leading to a lower barrier. However, since DFT is intrinsically a single Slater configuration, the mixing of the other states is not accounted for, leading to the overestimated barrier height.

In a follow up study, this group examined the thermal and photo cyclization of 13,14-dimethylcethrene 4.² The added methyl groups make the centhrene backbone more helical, and this precludes the formal allowed disrotatory process. The methyl groups also prohibit the oxidation that occurs with 1, driven by aromatization, allowing for the isolation of the direct product of the cyclization 5. This antistereochemistry is confirmed by NMR and x-ray crystallography. The interconversion between 4 and 5 can be controlled by heat and light, making the system an interesting photoswitch.

Also of interest is the singlet-triplet gap of 1 and 4. The DFT computed ΔE_ST is about 10 kcal mol^-1 for 4, larger than the computed value of 6 kcal mol^-1 for 1b. The EPR of 1b does show a signal while that of 4has no signal. To assess the role of the methyl group, they computed the singlet triplet gaps for 1b and 4at two different geometries: where the distance between the carbons bearing the methyl groups is that in 1b (3.03 Å) and in 4 (3.37 Å). The lengthening of this distance by the methyl substituents is due to increased helical twist in 4 than in 1b. For 1b, the gap increases with twisting, from 7.1 to 8.3 kcal mol^-1, while for 4 the gap increases by 1.8 kcal mol^-1 with the increased twisting. This change is less than the effect of methyl substitution, which increases the gap by 2.2 kcal mol^-1 at the shorter distance and 2.8 kcal mol^-1 at the longer distance. Thus, the electronic (orbital) effect of methyl substitution affects the singlet-triplet gap more than the geometric twisting.

References

1) Šolomek, T.; Ravat, P.; Mou, Z.; Kertesz, M.; Juríček, M., "Cethrene: The Chameleon of Woodward–Hoffmann Rules." J. Org. Chem. 2018, 83, 4769-4774, DOI: 10.1021/acs.joc.8b00656.

2) Ravat, P.; Šolomek, T.; Häussinger, D.; Blacque, O.; Juríček, M., "Dimethylcethrene: A Chiroptical Diradicaloid Photoswitch." J. Am. Chem. Soc. 2018, 140, 10839-10847, DOI: 10.1021/jacs.8b05465.

InChIs

1b: InChI=1S/C28H16/c1-5-17-7-3-11-23-25(17)19(9-1)15-21-13-14-22-16-20-10-2-6-18-8-4-12-24(26(18)20)28(22)27(21)23/h1-16H
InChIKey=GBMHAGKZRAVBDO-UHFFFAOYSA-N

4: InChI=1S/C30H20/c1-17-9-11-19-5-3-7-21-15-23-13-14-24-16-22-8-4-6-20-12-10-18(2)26(28(20)22)30(24)29(23)25(17)27(19)21/h3-16H,1-2H3
InChIKey=MXTVFWTUCPRNIW-UHFFFAOYSA-N

5: nChI=1S/C30H20/c1-29-13-11-17-5-3-7-19-15-21-9-10-22-16-20-8-4-6-18-12-14-30(29,2)28(24(18)20)26(22)25(21)27(29)23(17)19/h3-16H,1-2H3/t29-,30-/m0/s1
InChIKey=SUMMGEBJORQMAI-KYJUHHDHSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Evolving and nano data enabled machine intelligence for chemical reaction optimization

Daniel Reker, Gonçalo J. L. Bernardes, Tiago Rodrigues (2018)

Highlighted by Jan Jensen

This paper is probably on the edge of what most people would call computational chemistry in the sense that is doesn't deal with structure-based predictions. 

The paper uses a random forest algorithm to optimise reaction conditions. What is especially interesting is the small amount of data needed to train the model compared to other machine learning algorithms. The method starts with only 10 randomly chosen reaction conditions as input and goes on to find an optimum set of conditions in only 20 additional steps. This approach is tested against expert synthetic chemists and found to be just as good or better.

It is possible that this method could be adapted to molecular design (e.g. choosing the best combination of ligands) of properties that are expensive to compute or costly to measure experimentally.

The code is available here


This work is licensed under a Creative Commons Attribution 4.0 International License.

Carbo‐biphenyls and Carbo‐terphenyls: Oligo(phenylene ethynylene) Ring Carbo‐mers

Chongwei, Z.; Albert, P.; Carine, D.; Brice, K.; Alix, S.; Valérie, M.; Remi, C., Angew. Chem. Int. Ed. 2018, 57, 5640-5644
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Interesting 18 π-electron systems involving cyclooctadecanonenetriyne rings have been synthesized and examined by computations.¹ The mono-, di- and tri-C₁₈
ring compounds 1, 2, and 3 were prepared and the x-ray structure of 2 was obtained. The B3PW91/6-31G(d,p) optimized geometries of 1-3 and of the tetra ring 4 are shown in Figure 1.

1

2

3

4

Figure 1. B3PW91/6-31G(d,p) optimized geometries of 1-4.

Since the rings are composed of 18 π-electrons in the π-system perpendicular to the nearly planar ring, the natural question is to wonder if the ring is aromatic. The authors computed NICS(0) and NICS(1) values at the center of the C₁₈ rings. For all four compounds, both the NICS(0) and NICS(1) values are negative, ranging from -12.4 to -14.9 ppm, indicating that the rings are aromatic.

References

1) Chongwei, Z.; Albert, P.; Carine, D.; Brice, K.; Alix, S.; Valérie, M.; Remi, C., "Carbo‐biphenyls and Carbo‐terphenyls: Oligo(phenylene ethynylene) Ring Carbo‐mers." Angew. Chem. Int. Ed. 2018, 57, 5640-5644, DOI: 10.1002/anie.201713411.

InChIs

1: InChI=1S/C58H54/c1-3-5-7-9-11-17-27-49-37-41-55(51-29-19-13-20-30-51)45-47-57(53-33-23-15-24-34-53)43-39-50(28-18-12-10-8-6-4-2)40-44-58(54-35-25-16-26-36-54)48-46-56(42-38-49)52-31-21-14-22-32-52/h13-16,19-26,29-36H,3-12,17-18,27-28H2,1-2H3
InChIKey=KWXYBTWOEJBCQD-UHFFFAOYSA-N

2: InChI=1S/C102H74/c1-3-5-7-9-11-21-39-83-59-67-95(87-41-23-13-24-42-87)75-79-99(91-49-31-17-32-50-91)71-63-85(64-72-100(92-51-33-18-34-52-92)80-76-96(68-60-83)88-43-25-14-26-44-88)57-58-86-65-73-101(93-53-35-19-36-54-93)81-77-97(89-45-27-15-28-46-89)69-61-84(40-22-12-10-8-6-4-2)62-70-98(90-47-29-16-30-48-90)78-82-102(74-66-86)94-55-37-20-38-56-94/h13-20,23-38,41-56H,3-12,21-22,39-40H2,1-2H3
InChIKey=HHRPTZGYBIHFOL-UHFFFAOYSA-N

3: InChI=1S/C146H94/c1-3-5-7-9-11-25-51-117-81-93-135(123-53-27-13-28-54-123)105-109-139(127-61-35-17-36-62-127)97-85-119(86-98-140(128-63-37-18-38-64-128)110-106-136(94-82-117)124-55-29-14-30-56-124)77-79-121-89-101-143(131-69-43-21-44-70-131)113-115-145(133-73-47-23-48-74-133)103-91-122(92-104-146(134-75-49-24-50-76-134)116-114-144(102-90-121)132-71-45-22-46-72-132)80-78-120-87-99-141(129-65-39-19-40-66-129)111-107-137(125-57-31-15-32-58-125)95-83-118(52-26-12-10-8-6-4-2)84-96-138(126-59-33-16-34-60-126)108-112-142(100-88-120)130-67-41-20-42-68-130/h13-24,27-50,53-76H,3-12,25-26,51-52H2,1-2H3
InChIKey=WCBXPLIBHKYESX-UHFFFAOYSA-N

4: InChI=1S/C190H114/c1-3-5-7-9-11-29-63-151-103-119-175(159-65-31-13-32-66-159)135-139-179(163-73-39-17-40-74-163)123-107-153(108-124-180(164-75-41-18-42-76-164)140-136-176(120-104-151)160-67-33-14-34-68-160)97-99-155-111-127-183(167-81-47-21-48-82-167)143-147-187(171-89-55-25-56-90-171)131-115-157(116-132-188(172-91-57-26-58-92-172)148-144-184(128-112-155)168-83-49-22-50-84-168)101-102-158-117-133-189(173-93-59-27-60-94-173)149-145-185(169-85-51-23-52-86-169)129-113-156(114-130-186(170-87-53-24-54-88-170)146-150-190(134-118-158)174-95-61-28-62-96-174)100-98-154-109-125-181(165-77-43-19-44-78-165)141-137-177(161-69-35-15-36-70-161)121-105-152(64-30-12-10-8-6-4-2)106-122-178(162-71-37-16-38-72-162)138-142-182(126-110-154)166-79-45-20-46-80-166/h13-28,31-62,65-96H,3-12,29-30,63-64H2,1-2H3
InChIKey=LLVPDVPZEIYJGN-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation

Jiaxuan You, Bowen Liu, Rex Ying, Vijay Pande, Jure Leskovec (2018)

Highlighted by Jan Jensen



Ever since Alán Aspuru-Guzik and co-workers published their seminal paper there has been a flurry of activity on generative models, which is not surprising given that they offer a radically new alternative to screening chemical libraries as a way to discover new molecules.

Almost all the new efforts on generative models have been based on adapting machine learning techniques used for natural language processing to text-based representation of molecules, i.e. SMILES strings. While very promising the SMILES syntax has some quirks which makes them hard to predicts efficiently. One solution is to change the syntax to be more ML-friendly, but this has yet to be tested for generative models.

Another option is to work with a graph (i.e. atoms and bonds) representation of the molecule and this paper is the first I've seen that does that for an ML-based generative model. In this case the ML method is reinforcement learning where the addition of each atom is treated as an action which can be trained to towards a particular outcome, here molecules with certain properties. This approach seems to outperform the SMILES based approaches for the prediction of some properties.

The code is available here.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Teaching an old carbocation new tricks: Intermolecular C–H insertion reactions of vinyl cations

Popov, S.; Shao, B.; Bagdasarian, A. L.; Benton, T. R.; Zou, L.; Yang, Z.; Houk, K. N.; Nelson, H. M., Science 2018, 361, 381
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

A recent paper by Papov, Shao, Bagdasarian, Benton, Zou, Yang, Houk, and Nelson uncovers a vinyl cation insertion reaction that once again involves dynamic effects.¹

They find that vinyl triflates and cyclic vinyl triflates will react with [Ph₃C]⁺[HCB₁₁Cl₁₁]^– and triethylsilane to generate vinyl cations that can then be trapped through a C-H insertion reaction. For example, cyclohexenyl triflate 1 reacts in a cyclohexane solvent to give the insertion product 2.

The reactions of isomers 3 and 4 give different ratios of the two products 5 and 6. In both cases, the cyclohexyl is trapped predominantly at the site of the triflate substituent. This means that the mechanism cannot involve a cyclohexene intermediate, since then the two ratios should be identical.

They performed molecular dynamic trajectory analysis at the M062X/6-311+G(d,p) level, starting with the two transition states leading from 3 (TS3) and 4 (TS4), the only transition states located for the insertion reaction. The structures of these TSs are shown in Figure 1.

TS3

TS4

Figure 1. M062X/6-311+G(d,p) optimized geometries of TS3 and TS4.

The trajectories end up in two product basins associated with 5 and 6 starting with either TS3 or TS4. Thus, these transition states are ambimodal, and typical of reactions where dynamic effects dominate. For the reaction of 3, the majority of the trajectories starting at TS3 end up as 5, consistent with the experiments. Similarly, for the trajectories that start at TS4, the majority end up as 6, consistent with experiments.

Once again, we see that relatively simple organic reactions do not follow simple reaction mechanisms, that a single transition state leads to two different products and the product distributions are dependent on reaction dynamics. This may not be too surprising for the vinyl cation insertions given the many examples provide by the Tantillo group of cation rearrangements that are controlled by reaction dynamics (see for examples, this post and this post).

References

1. Popov, S.; Shao, B.; Bagdasarian, A. L.; Benton, T. R.; Zou, L.; Yang, Z.; Houk, K. N.; Nelson, H. M., "Teaching an old carbocation new tricks: Intermolecular C–H insertion reactions of vinyl cations." Science2018, 361, 381-387, DOI: 10.1126/science.aat5440.

InChIs

1: InChI=1S/C7H10F3O3S/c8-7(9,10)14(11,12,13)6-4-2-1-3-5-6/h4H,1-3,5H2,(H,11,12,13)
InChIKey=CMPVYBNXADJVOM-UHFFFAOYSA-N

2: InChI<=1S/C12H22/c1-3-7-11(8-4-1)12-9-5-2-6-10-12/h11-12H,1-10H2
InChIKey=WVIIMZNLDWSIRH-UHFFFAOYSA-N

3: InChI=1S/C9H14F3O3S/c1-8(2)5-3-7(4-6-8)16(13,14,15)9(10,11)12/h3H,4-6H2,1-2H3,(H,13,14,15)
InChIKey=XDWBLRRAHKBZJR-UHFFFAOYSA-N

4: InChI=1S/C9H14F3O3S/c1-8(2)5-3-4-7(6-8)16(13,14,15)9(10,11)12/h4H,3,5-6H2,1-2H3,(H,13,14,15)
InChIKey=YHVCPSRICQJFDT-UHFFFAOYSA-N

5: InChI=1S/C14H26/c1-14(2)10-8-13(9-11-14)12-6-4-3-5-7-12/h12-13H,3-11H2,1-2H3
InChIKey=BZQBWUOXOYWYJC-UHFFFAOYSA-N

6: InChI=1S/C14H26/c1-14(2)10-6-9-13(11-14)12-7-4-3-5-8-12/h12-13H,3-11H2,1-2H3
InChIKey=AENMAOBTECURBO-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

DeepSMILES: An adaptation of SMILES for use in machine-learning of chemical structures

Noel M. O’Boyle and Andrew Dalke (2018)

Highlighted by Jan Jensen



There's been a lot of work in the last few years on machine learning methods for suggesting molecules (see here and here for examples). Most of these "generative models" are trained using  SMILES representations of the molecules. But SMILES was never designed with machine learning in mind and contain features that can cause problems when doing so. The end result is that generative models suggest a lot of SMILES strings with the wrong syntax. For example CC(C(C instead of CC(C)C.

Noel and Andrew suggest a different SMILES syntax (DeepSMILES) that addresses many of these problems. Have a look at the figure above to see if you can deduce the conversion-rules and read the paper to see close you got. It will be very interesting to see whether DeepSMILES will lead to significant improvements in machine learning applications.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Curved Aromatic molecules – 4 new examples

Contributed by Steven Bacharach

Reposted from Computational Organic Chemistry with permission

I have recently been interested in curved aromatic systems – see my own paper on double helicenes.¹ In this post, I cover four recent papers that discuss non-planar aromatic molecules.

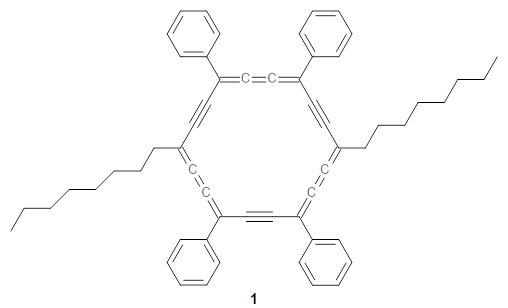
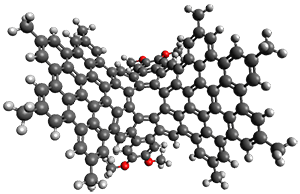
The first paper² discusses the warped aromatic 1 built off of the scaffold of depleiadene 3. The crystal structure of 1 shows the molecule to be a saddle with near C_2v symmetry. B3LYP/6-31G computations indicate that the saddle isomer is 10.5 kcal mol^-1 more stable than the twisted isomer, and the barrier between them is 16.0 kcal mol^-1, with a twisted saddle intermediate as well.

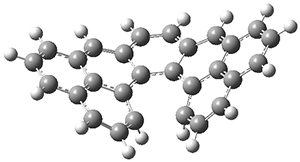
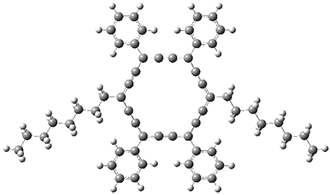
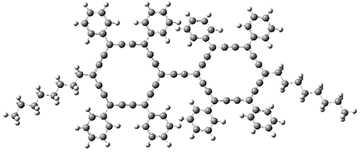
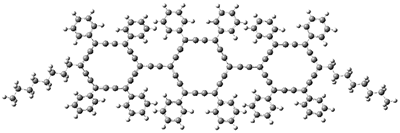
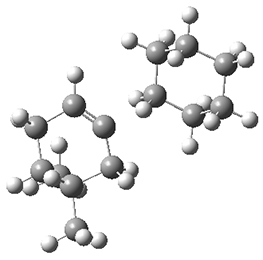
The PES is significantly simpler for the structure lacking the t-butyl groups, 2. The B3LYP/6-31G PES of 2has the saddle as the transition state interconverting mirror images of the twisted saddle isomer, and this barrier is only 1.8 kcal mol^-1. Figure 1 displays the twisted saddle and the saddle transition state. Clearly, the t-butyl groups significantly alter the flexibility of this C₈₆ aromatic surface. One should be somewhat concerned about the small basis set employed here, especially lacking polarization functions, and a functional that lacks dispersion correction. However, the computed geometry of 1 is quite similar to that of the x-ray structure.

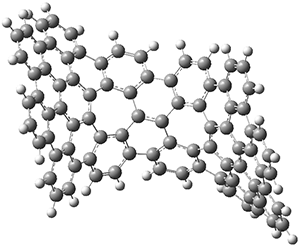2 twisted saddle (ground state)

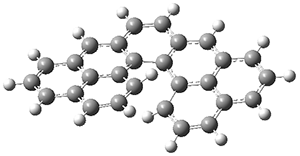
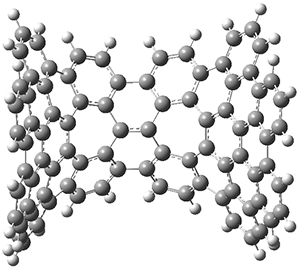2 saddle (transition state)

Figure 1. B3LYP/6-31G optimized geometries of the isomer of 2.

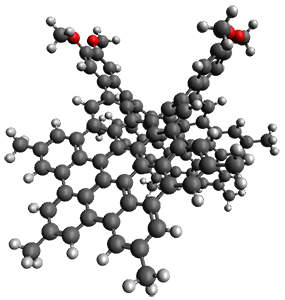
The second paper presents 4, a non-planar aromatic based on [8]circulene 6.³ (See this post for a general study of circulenes.) [8]circulene has a tub-shape, but is flexible and can undergo tub-to-tub inversion. The expanded aromatic 4 is found to have a twisted shape in the x-ray crystal structure. A simplified model 5 was computed at B3LYP/6-31G(d) and the twisted isomer is 4.1 kcal mol^-1 lower in energy than the saddle (tub) isomer (see Figure 2). The barrier for interconversion of the two isomers is only 6.2 kcal mol^-1, indicating a quite labile structure.

5 twisted 0.0

5 TS 6.2

5 saddle 4.1

Figure 2. B3LYP/6-31G(d) optimized geometries and relative energies (kcal mol^-1) of the isomers of 5.

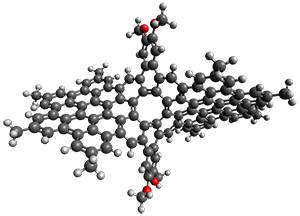
The third paper presents a geodesic molecule based on 1,3,5-trisubstitued phenyl repeat units.⁴ The authors prepared 7, and its x-ray structure shows a saddle-shape. The NMR indicate a molecule that undergoes considerable conformational dynamics. To address this, they did some computations on the methyl analogue 8. The D_7h structure is 309 kcal mol^-1 above the local energy minimum structure, which is way too high to be accessed at room temperature. 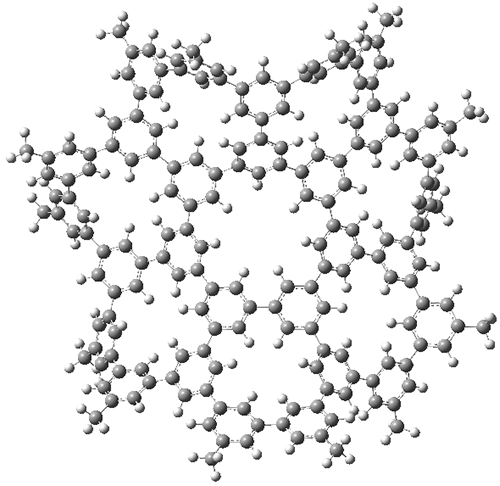PM6 computations identified a TS only 0.6 kcal mol^-1above the saddle ground state. (I performed a PM6 optimization starting from the x-ray structure, which is highly disordered, and the structure obtained is shown in Figure 3. Unfortunately, the authors did not report the optimized coordinates of any structure!)

Figure 3. PM6 optimized structure of 8.

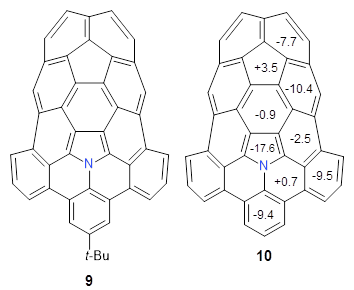
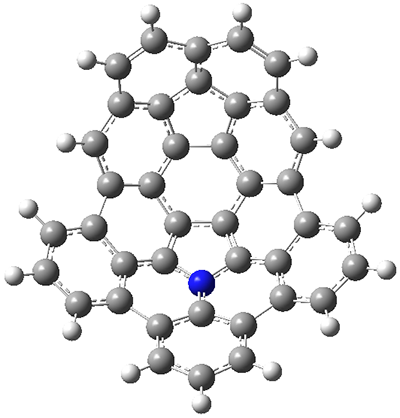
The fourth and last paper describes the aza-buckybowl 9.⁵ The x-ray crystal structure shows a curved bowl shape with C_s symmetry. NICS(0) values were computed for the parent molecule 10 B3LYP/6-31G(d). These values are shown in Scheme 1 and the geometry is shown in Figure 4. The 6-member rings that surround the azacylopentadienyl ring all have NICS(0) near zero, which suggests significant bond localisation.

Scheme 1. NICS(0) values of 10

Figure 4. B3LYP/6-31G(d) optimized structure of 10.

Our understanding of what aromaticity really means is constantly being challenged!

References

1. Bachrach, S. M., "Double helicenes." Chem. Phys. Lett. 2016, 666, 13-18, DOI: 10.1016/j.cplett.2016.10.070.

2. Ho, P. S.; Kit, C. C.; Jiye, L.; Zhifeng, L.; Qian, M., "A Dipleiadiene-Embedded Aromatic Saddle Consisting
of 86 Carbon Atoms." Angew. Chem. Int. Ed. 2018, 57, 1581-1586, DOI: 10.1002/anie.201711437.

3. Yin, C. K.; Kit, C. C.; Zhifeng, L.; Qian, M., "A Twisted Nanographene Consisting of 96 Carbon Atoms." Angew. Chem. Int. Ed. 2017, 56, 9003-9007, DOI: 10.1002/anie.201703754.

4. Koki, I.; Jennie, L.; Ryo, K.; Sota, S.; Hiroyuki, I., "Fluctuating Carbonaceous Networks with a Persistent
Molecular Shape: A Saddle-Shaped Geodesic Framework of 1,3,5-Trisubstituted Benzene (Phenine)." Angew. Chem. Int. Ed. 2018, 57, 8555-8559, DOI: 10.1002/anie.201803984.

5. Yuki, T.; Shingo, I.; Kyoko, N., "A Hybrid of Corannulene and Azacorannulene: Synthesis of a Highly Curved Nitrogen-Containing Buckybowl." Angew. Chem. Int. Ed. 2018, 57, 9818-9822, DOI: 10.1002/anie.201805678.

InChIs

1: InChI=1S/C134H128/c1-123(2,3)57-37-65-66-38-58(124(4,5)6)42-70-74-46-62(128(16,17)18)50-82-94(74)110-106(90(66)70)105-89(65)69(41-57)73-45-61(127(13,14)15)49-81-93(73)109(105)119-113-97(81)85(131(25,26)27)53-77-78-54-87(133(31,32)33)99-83-51-63(129(19,20)21)47-75-71-43-59(125(7,8)9)39-67-68-40-60(126(10,11)12)44-72-76-48-64(130(22,23)24)52-84-96(76)112-108(92(68)72)107(91(67)71)111(95(75)83)121-115(99)103(78)118-104-80(56-88(134(34,35)36)100(84)116(104)122(112)121)79-55-86(132(28,29)30)98(82)114(120(110)119)102(79)117(118)101(77)113/h37-56H,1-36H3
InChIKey=GKUTUWMASUJSFD-UHFFFAOYSA-N

2: InChI=1S/C86H32/c1-9-33-34-10-2-14-38-42-18-6-22-46-50-26-30-55-56-32-28-52-48-24-8-20-44-40-16-4-12-36-35-11-3-15-39-43-19-7-23-47-51-27-31-54-53-29-25-49-45-21-5-17-41-37(13-1)57(33)73-74(58(34)38)78(62(42)46)84-70(50)66(55)81(65(53)69(49)83(84)77(73)61(41)45)82-67(54)71(51)85-79(63(43)47)75(59(35)39)76(60(36)40)80(64(44)48)86(85)72(52)68(56)82/h1-32H
InChIKey=MXCDWJZMTKLBDM-UHFFFAOYSA-N

3: InChI=1S/C18H12/c1-2-6-14-11-12-16-8-4-3-7-15-10-9-13(5-1)17(14)18(15)16/h1-12H
InChIKey=KVJJNMIHWIRGRP-UHFFFAOYSA-N

4: InChI=1S/C132H108O4/c1-125(2,3)53-29-65-66-30-54(126(4,5)6)34-70-74-38-58(130(16,17)18)42-78-86-46-82-63-51-91(135-27)92(136-28)52-64(63)84-48-88-80-44-60(132(22,23)24)40-76-72-36-56(128(10,11)12)32-68-67-31-55(127(7,8)9)35-71-75-39-59(131(19,20)21)43-79-87-47-83-62-50-90(134-26)89(133-25)49-61(62)81-45-85-77-41-57(129(13,14)15)37-73-69(33-53)93(65)109-110(94(66)70)114(98(74)78)122-106(86)118-103(82)104(84)120-108(88)124-116(100(76)80)112(96(68)72)111(95(67)71)115(99(75)79)123(124)107(87)119(120)102(83)101(81)117(118)105(85)121(122)113(109)97(73)77/h29-52H,1-28H3
InChIKey=ZLPRACZKLACDHX-UHFFFAOYSA-N

5: InChI=1S/C108H60O4/c1-37-13-49-50-14-38(2)18-54-58-22-42(6)26-62-70-30-66-47-35-75(111-11)76(112-12)36-48(47)68-32-72-64-28-44(8)24-60-56-20-40(4)16-52-51-15-39(3)19-55-59-23-43(7)27-63-71-31-67-46-34-74(110-10)73(109-9)33-45(46)65-29-69-61-25-41(5)21-57-53(17-37)77(49)93-94(78(50)54)98(82(58)62)106-90(70)102-87(66)88(68)104-92(72)108-100(84(60)64)96(80(52)56)95(79(51)55)99(83(59)63)107(108)91(71)103(104)86(67)85(65)101(102)89(69)105(106)97(93)81(57)61/h13-36H,1-12H3
InChIKey=ZSIVUKSPPZUSQL-UHFFFAOYSA-N

6: InChI=1S/C32H16/c1-2-18-5-6-20-9-11-22-13-15-24-16-14-23-12-10-21-8-7-19-4-3-17(1)25-26(18)28(20)30(22)32(24)31(23)29(21)27(19)25/h1-16H
InChIkey=BASWMOIVIHXTRC-UHFFFAOYSA-N

7: InChI=1S/C224H210/c1-211(2,3)197-99-169-85-183(113-197)184-86-170(100-198(114-184)212(4,5)6)157-66-149-67-158(79-157)172-88-187(117-200(102-172)214(10,11)12)188-90-174(104-202(118-188)216(16,17)18)161-70-151-71-162(81-161)176-92-191(121-204(106-176)218(22,23)24)193-95-179(109-207(123-193)221(31,32)33)165-74-153-75-166(83-165)180-96-195(125-208(110-180)222(34,35)36)196-98-182(112-210(126-196)224(40,41)42)168-77-154-76-167(84-168)181-97-194(124-209(111-181)223(37,38)39)192-94-178(108-206(122-192)220(28,29)30)164-73-152-72-163(82-164)177-93-190(120-205(107-177)219(25,26)27)189-91-175(105-203(119-189)217(19,20)21)160-69-150-68-159(80-160)173-89-186(116-201(103-173)215(13,14)15)185-87-171(101-199(115-185)213(7,8)9)156-65-148(64-155(169)78-156)141-50-127-43-128(51-141)130-45-132(55-143(150)53-130)134-47-136(59-145(152)57-134)138-49-140(63-147(154)61-138)139-48-137(60-146(153)62-139)135-46-133(56-144(151)58-135)131-44-129(127)52-142(149)54-131/h43-126H,1-42H3
InChIKey=ZDDKJXIESSWTIA-UHFFFAOYSA-N

8: InChI=1S/C182H126/c1-99-15-113-43-127(29-99)141-57-142-65-155(64-141)162-78-169-92-170(79-162)172-82-164-83-174(94-172)176-85-166-87-178(96-176)180-89-168-91-182(98-180)181-90-167-88-179(97-181)177-86-165-84-175(95-177)173-81-163(80-171(169)93-173)156-66-143(128-30-100(2)16-114(113)44-128)58-144(67-156)130-32-103(5)19-117(47-130)118-20-104(6)34-132(48-118)147-60-148(71-158(165)70-147)134-36-107(9)23-121(51-134)123-25-109(11)39-137(53-123)151-62-152(75-160(167)74-151)138-40-111(13)27-125(55-138)126-28-112(14)42-140(56-126)154-63-153(76-161(168)77-154)139-41-110(12)26-124(54-139)122-24-108(10)38-136(52-122)150-61-149(72-159(166)73-150)135-37-106(8)22-120(50-135)119-21-105(7)35-133(49-119)146-59-145(68-157(164)69-146)131-33-102(4)18-116(46-131)115-17-101(3)31-129(142)45-115/h15-98H,1-14H3
InChIKey=FJHGGHOTCCNJNI-UHFFFAOYSA-N

9: InChI=1S/C44H23N/c1-44(2,3)21-16-28-24-8-4-6-22-26-14-19-12-10-18-11-13-20-15-27-23-7-5-9-25-29(17-21)41(28)45-42(33(22)24)39-35(26)37-31(19)30(18)32(20)38(37)36(27)40(39)43(45)34(23)25/h4-17H,1-3H3
InChIKey=QHBWEZKXFSKCSM-UHFFFAOYSA-N

10: InChI=1S/C40H15N/c1-4-19-23-8-3-9-24-20-5-2-7-22-26-15-18-13-11-16-10-12-17-14-25-21(6-1)30(19)39-36-32(25)34-28(17)27(16)29(18)35(34)33(26)37(36)40(31(20)22)41(39)38(23)24/h1-15H
InChIKey=XWSUADIIRLXSBY-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Rearrangement of Hydroxylated Pinene Derivatives to Fenchone-Type Frameworks: Computational Evidence for Dynamically-Controlled Selectivity

Blümel, M.; Nagasawa, S.; Blackford, K.; Hare, S. R.; Tantillo, D. J.; Sarpong, R., J. Am. Chem. Soc. 2018, 140, 9291-9298
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Sarpong and Tantillo have examined the acid-catalyzed Prins/semipinacol rearrangement of hydroxylated pinenes, such as Reaction 1.¹

Rxn 1

Interestingly, only the fenchone scaffold products, like 1, are observed and the camphor scaffold products, like 2, are not observed. Cation intermediates are likely, and this means that a primary alkyl shift is taking place in preference to a tertiary alkyl shift, see Scheme 1.

Scheme 1.

Primary alkyl shift

Tertiary alkyl shift

They proposed the following key steps in the reaction mechanism:

ωB97X-D/6-31+G(d,p) computations find a flat surface around cation intermediate 4: the TS leading to 5and 6 are only 1.3 and 3.3 kcal mol^-1, respectively. Since these small barriers are quite susceptible to changes in basis set and functional, and since Tantillo has found many examples of post-transition state bifurcations in cation systems, the authors reasonably decided to conduct molecular dynamics trajectories originating at the TS connecting 3 and 4. The geometries of the critical points are shown in Figure 1.

The trajectory study shows all the usual characteristics of reactions that are under dynamic control. A third of the trajectories show recrossing of the barrier, typical of very flat surfaces. Nearly all of the remaining trajectories led to 5, with only 2 trajectories (~1%) leading to 6. The dynamics are understandable in terms of favoring the primary alkyl shift over the tertiary since a significantly smaller mass needs to move in the former case.

TS 3 → 4
4
TS 4 → 5	TS 4 → 6

Figure 1. ωB97X-D/6-31+G(d,p) optimized geometries.

This is yet another study that implicates dynamic effects in routine reactions, one of many I have discussed over the years.

References

1. Blümel, M.; Nagasawa, S.; Blackford, K.; Hare, S. R.; Tantillo, D. J.; Sarpong, R., "Rearrangement of Hydroxylated Pinene Derivatives to Fenchone-Type Frameworks: Computational Evidence for Dynamically-Controlled Selectivity." J. Am. Chem. Soc. 2018, 140, 9291-9298, DOI: 10.1021/jacs.8b05804.

InChIs

1: InChI=1S/C17H20O2/c1-16-9-12-8-13(16)14(11-6-4-3-5-7-11)19-10-17(12,2)15(16)18/h3-7,12-14H,8-10H2,1-2H3/t12?,13?,14-,16?,17?/m0/s1
InChIKey=LTTUIPPXEHHMJS-XWTIBIIYSA-N

2: InChI=1S/C17H20O2/c1-16-10-19-15(11-6-4-3-5-7-11)13-8-12(16)9-14(18)17(13,16)2/h3-7,12-13,15H,8-10H2,1-2H3/t12?,13?,15-,16?,17?/m0/s1
InChIKey=GCKIOHNLJYVWKL-CMESGNGWSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

A Density Functional Tight Binding Layer for Deep Learning of Chemical Hamiltonians

Haichen Li, Christopher Collins, Matteus Tanha, Geoffrey J. Gordon, David J. Yaron (2018)
Highlighted by Jan Jensen

There are increasingly many papers on predicting the molecular energy and other properties using machine learning (ML). Most, if not all, use some similarity measure of the molecular structure to structures in the training set when training. This paper uses DFTB Hamiltonian matrix elements instead and treats the short-range matrix elements as adjustable parameters (weights) to be trained. To make this happen, DFTB is implemented as a layer for deep learning, using the TensorFlow deep learning framework, by recasting the DFTB equations in terms of tensor operations. In this way domain knowledge is incorporated into the ML model. Since the starting values are the "conventional" DFTB parameters one can also view this as refining the DFTB method.

This DFTB-ML approach is evaluated on 15,700 hydrocarbons by comparing the RMSE in energy per heavy atom (Eatom) relative to ωB97X/6-31G(d) reference values. Training on up to 7 heavy atoms and testing on 8 heavy atoms, leads to RMS errors in Eatom of 0.72 kcal/mol, compared to 1.80 using conventional DFTB. Training on up to 4 heavy atoms gives an Eatom RMSE of 1.08 kcal/mol. The results can be further improved by using neural networks to allow the matrix elements to depend on the molecular environment of the atoms.

As the authors point out the performance on the training data remained above chemical accuracy (0.5 kcal/mol) for the total molecular energy, but they offer several interesting ideas on how to improve the performance.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Nano-Saturn: Experimental Evidence of Complex Formation of an Anthracene Cyclic Ring with C60

Yuta, Y.; Eiji, T.; Kan, W.; Shinji, T., Angew. Chem. Int. Ed. 2018, 57, 8199-8202
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

It never hurts to promote one’s science through clever names – think cubane, buckminsterfullerene, bullvalene, etc. Host-guest chemistry is not immune to this cliché too, and this post discusses the latest synthesis and computations of a nano-Saturn; nano-Saturns are a spherical guest molecule captured inside a ring host molecule. I discussed an example of this a number of years ago – the nano-Saturn comprised of C₆₀ fullerene surrounded by [10]cycloparaphenylene.

Yamamoto, Tsurumaki, Wakamatsu, and Toyota have prepared a nano-Saturn complex with the goal of making a flatter ring component.¹ The inner planet is modeled again by C₆₀ and the ring is the [24]circulene analogue 1. The x-ray crystal structure of this nano-Saturn complex is shown in Figure 1.

1: R = 2,4,6-tri-iso-propylphenyl
2: R = H

Figure 1. X-ray crystal structure of the nano-Saturn complex of 1 with C₆₀.

Variable temperature NMR experiments gave the binding values of ΔH = -18.1 ± 2.3 kJ mol^-1 and TΔS = 0.8 ± 2.2 kJ mol^-1 at 298 K. To gauge this binding energy, they computed the complex of C₆₀ with the parent compound 2 at B3LYP/6-1G(d)//M05-2X/6-31G(d), unfortunately without publishing the coordinates in the supporting materials. The computed binding enthalpy is ΔH = -50.6 kJ mol^-1, but this computation is for the gas phase. The computed structure shows close contacts of 0.29 nm between the fullerene and the C₉-proton of the anthracenyl groups, in excellent agreement with the x-ray structure. These weak C-H^…π interactions undoubtedly help stabilize the complex, especially given that the fullerene carries a very tiny Mulliken charge of +0.08 e.

References

1) Yuta, Y.; Eiji, T.; Kan, W.; Shinji, T., "Nano-Saturn: Experimental Evidence of Complex Formation of an Anthracene Cyclic Ring with C60." Angew. Chem. Int. Ed. 2018, 57, 8199-8202, DOI: 10.1002/anie.201804430.

InChIs

1: InChI=1S/C174H180/c1-91(2)121-78-150(97(13)14)164(151(79-121)98(15)16)163-90-128-71-139-70-127-59-109(37-38-120(127)77-162(139)163)110-39-49-140-129(60-110)72-130-61-111(40-50-141(130)165(140)170-152(99(17)18)80-122(92(3)4)81-153(170)100(19)20)112-41-51-142-131(62-112)73-132-63-113(42-52-143(132)166(142)171-154(101(21)22)82-123(93(5)6)83-155(171)102(23)24)114-43-53-144-133(64-114)74-134-65-115(44-54-145(134)167(144)172-156(103(25)26)84-124(94(7)8)85-157(172)104(27)28)116-45-55-146-135(66-116)75-136-67-117(46-56-147(136)168(146)173-158(105(29)30)86-125(95(9)10)87-159(173)106(31)32)118-47-57-148-137(68-118)76-138-69-119(128)48-58-149(138)169(148)174-160(107(33)34)88-126(96(11)12)89-161(174)108(35)36/h37-108H,1-36H3
InChIKey=AMDNULXMAMDTMX-UHFFFAOYSA-N

2: InChI=1S/C84H48/c1-13-61-25-62-15-3-51-33-75(62)43-73(61)31-49(1)50-2-14-63-26-64-16-4-52(34-76(64)44-74(63)32-50)54-6-18-66-28-68-20-8-56(38-80(68)46-78(66)36-54)58-10-22-70-30-72-24-12-60(42-84(72)48-82(70)40-58)59-11-23-71-29-69-21-9-57(39-81(69)47-83(71)41-59)55-7-19-67-27-65-17-5-53(51)35-77(65)45-79(67)37-55/h1-48H
InChIKey=ZYXXLAYETADMDM-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.