Towards First Principles Calculation of Electron Impact Mass Spectra of Molecules

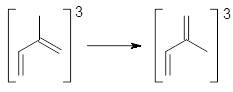
Stefan Grimme Angew. Chem. Int. Ed. 2013, 52, 6306
Contributed by +Jan Jensen

Quantum chemistry has contributed significantly to nearly all spectroscopic methods used in chemistry, but comparatively less so for mass spectrometry.  This might be about to change thanks to this very interesting study by Stefan Grimme.

Grimme presents a new program called QCEIMS, which together with the quantum programs ORCA, DFTB+, and MNDO, is used to predict electron impact mass spectra of molecules in a black box fashion.

The method starts with a ca 50 ps equilibrated ground state NVE Born-Oppenheimer MD simulation of the neutral molecule (M) using, for example, OM2 or DFTB3 (typically at 500 K).

The ionization from electron impact is simulated by randomly choosing a number of snapshots as starting points for new 5-10 ps NVE MD simulations with excess thermal energy.  Unrestricted, fractional occupation number wavefunctions are used and excess thermal energy is applied at the first step of each MD.  OM2 or DFTB3 can usually be used but KS-DFT/DZ may be necessary for cases where the fragmentations involve complex reaction mechanisms.

The charged fragments in the resulting "hot ion" ensemble are then identified and counted to yield the mass spectrum. Roughly 1-100 million energy and gradient evaluations are needed for good agreement with experimental spectra.


This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Evaluation of Triplet Aromaticity by the Isomerization Stabilization Energy

Zhu, J.; An, K.; Schleyer, P. v. R. Org. Lett. 2013, 15, 2442
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

One of the most widely recognized principles within organic chemistry is Hückel’s rule: an aromatic compound possesses 4n+2 π-electrons while an antiaromatic compound possesses 4n π-electrons. Much less well known is Baird’s rule:¹ the first excited triplet state will be aromatic if it has 4n π-electrons and antiaromatic if it has 4n+2 π-electrons.²

Schleyer used a number of standard methods for assessing aromatic character of a series of excited state triplets, including NICS values and geometric parameters.³ However, Schleyer has long been a proponent of an energetic assessment of aromaticity and it is only now in this recent paper⁴ that he and co-workers examine the stabilization energy of excited triplet states. The isomerization stabilization energy (ISE)⁵ compares an aromatic (or antiaromatic) compound against a non-aromatic reference, one that typically is made by appending an exo-methylene group to the ring. So, to assess the ISE of the T₁ state of benzene, Reaction 1 is used. (Note that the inherent assumption here is that the stabilization energy of benzene is essentially identical to that of toluene.) At B3LYP/6-311++G(d,p) the energy of Reaction 1 is +13.5 kcal mol^-1. This reaction should be corrected for non-conservation of s-cis and s-trans conformers by adding on the energy of Reaction 2, which is +3.4 kcal mol^-1. So, the ISE of triplet benzene is +16.9 kcal mol^-1, indicating that it is antiaromatic. In contrast, the ISE for triplet cyclooctatetraene is -15.6 kcal mol^-1, and when corrected its ISE value is -24.7 kcal mol^-1, indicatingaromatic character. These are completely consistent with Baird’s rule. Schleyer also presents an excellent correlation between the computed ISE values for the triplet state of 9 monocyclic polyenes and their NICS(1)_zz values.

	Reaction 1
	Reaction 2

I want to thank Henrik Ottosson for bringing this paper to my attention and for his excellent seminar on the subject of Baird’s rule on his recent visit to Trinity University.

References

(1) Baird, N. C. "Quantum organic photochemistry. II. Resonance and aromaticity in
the lowest 3ππ* state of cyclic hydrocarbons," J. Am. Chem. Soc. 1972, 94, 4941-4948, DOI:10.1021/ja00769a025.

(2) Ottosson, H. "Organic photochemistry: Exciting excited-state aromaticity," Nat Chem 2012, 4, 969-971, DOI: 10.1038/nchem.1518.

(3) Gogonea, V.; Schleyer, P. v. R.; Schreiner, P. R. "Consequences of Triplet Aromaticity in 4nπ-Electron Annulenes: Calculation of Magnetic Shieldings for Open-Shell Species," Angew. Chem. Int. Ed. 1998, 37, 1945-1948, DOI: 10.1002/(SICI)1521-3773(19980803)37:13/14<1945::AID-ANIE1945>3.0.CO;2-E.

(4) Zhu, J.; An, K.; Schleyer, P. v. R. "Evaluation of Triplet Aromaticity by the
Isomerization Stabilization Energy," Org. Lett. 2013, 15, 2442-2445, DOI: 10.1021/ol400908z.

(5) Schleyer, P. v. R.; Puhlhofer, F. "Recommendations for the Evaluation of Aromatic Stabilization Energies," Org. Lett. 2002, 4, 2873-2876, DOI: 10.1021/ol0261332.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Tunneling in the Bergman Cyclization

Greer, E. M.; Cosgriff, C. V.; Doubleday, C. J. Am. Chem. Soc. DOI: 10.1021/ja402445a

Contributed by Dean Tantillo

Edyta Greer and Christopher Cosgriff, in collaboration with Chuck Doubleday, have reported a quantum chemical study of the Bergman reaction of cyclodec-3-en-1,5-diyne (below). Using DFT and CASSCF calculations, they found evidence for a large contribution from heavy atom tunneling to the rate of this reaction even above room temperature.  

The performance of several levels of theory was examined, including a modified BLYP functional (mBLYP) and CCSD(T) on CASSCF geometries; the mBLYP/CASSCF method performed best.  Multidimensional tunneling effects were treated using the small curvature tunneling (SCT) approach in POLYRATE.  

It was predicted that at 200K, 60% of the rate is due to tunneling.  Moreover, the bulk of the tunneling was predicted to originate from energy levels within 2.3 kcal/mol of the transition state.  At temperatures between 310-350K a smaller energy range is predicted (~1.5 kcal/mol), which corresponds to only small changes in the length of the forming C-C bond (<0.2 Å) from its value at the transition state (this energy range is also smaller for wider barriers).  At these temperatures, rate enhancements of >30% due to tunneling were predicted.  

Experimentally testable predictions of the 12-C/13-C kinetic isotope effect at various temperatures were also made. This work not only puts some meat on the bones of various concepts associated with heavy atom tunneling, it also issues a challenge to experimentalists.

Enantioselective Thiourea-Catalyzed Intramolecular Cope-Type Hydroamination

Brown, A. R.; Uyeda, C.; Brotherton, C. A.; Jacobsen, E. N. J. Am. Chem. Soc. 2013, 135, 6747
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Jacobsen reports on another application of thiourea-based organocatalysts, this time for the catalysis of hydroamination.¹ To support the synthetic effort, he examined the uncatalyzed intramolecular hydroamination that takes 1, through TS1 into product 2. The geometry of TS1 optimized at B3LYP/6-31+G(d,p) is shown in Figure 1. The computed barrier for this reaction is 22.2 kcal mol^-1. Using a model thiourea as the catalyst (MeHN)₂C=S, 3), Jacobsen locates a catalyzed transition state TS2 shown in Figure 1. The activation barrier for this catalyzed reaction is 19.1 kcal mol^-1, suggesting that a thiourea can afford a real catalytic effect.

TS1

TS2

Figure 1. B3LYP/6-31+G(d,p) optimized geometries of TS1 and TS2(the catalyzed transition state).

Jacobsen then goes on to show that 4 can act as both an excellent catalyst for the hydroamination reaction along with inducing significant enantioselectivity. An example is Reaction 1, where 10 mol% of catalyst 3 gives an overall yield of 83% and an ee of 91%, while in the absence of catalyst the yield is only 8%.

References

(1) Brown, A. R.; Uyeda, C.; Brotherton, C. A.; Jacobsen, E. N. "Enantioselective Thiourea-Catalyzed Intramolecular Cope-Type Hydroamination," J. Am. Chem. Soc. 2013, 135, 6747-6749, DOI:10.1021/ja402893z.

InChIs

1: InChI=1S/C5H11NO/c1-2-3-4-5-6-7/h2,6-7H,1,3-5H2
InChIKey=JUMXQRNWLGIKEI-UHFFFAOYSA-N

2: InChI=1S/C5H11NO/c1-5-3-2-4-6(5)7/h5,7H,2-4H2,1H3
InChIKey=YVBPNYXAQNAMLH-UHFFFAOYSA-N

3: InChI=1S/C3H8N2S/c1-4-3(6)5-2/h1-2H3,(H2,4,5,6)
InChIKey=VLCDUOXHFNUCKK-UHFFFAOYSA-N

4: InChI=1S/C44H49N3OS/c1-44(2,3)42(41(48)36-25-15-24-35(36)34-23-14-21-30-16-10-11-22-33(30)34)46-43(49)45-37-26-12-13-27-40(37)47-38(31-17-6-4-7-18-31)28-29-39(47)32-19-8-5-9-20-32/h4-11,14,16-23,28-29,35-37,40,42H,12-13,15,24-27H2,1-3H3,(H2,45,46,49)/t35-,36?,37-,40-,42-/m1/s1
InChIKey=OJMZMPGOFWBKAF-FDGFXIECSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Will molecular dynamics simulations of proteins ever reach equilibrium

Samuel Genheden, Ulf Ryde. Phys. Chem. Chem.Phys., 2012, 14, 8662-8677

Contributed by Gerald Monard

When one runs molecular dynamics simulations, one always wonders whether the trajectories are “long enough”. The ergodic hypothesis states that with an infinite trajectory (in time), all accessible states should be reached. However, one cannot wait an infinite amount of time. In practice, trajectories are finite. Thus the question: did my molecular dynamics simulation have reach equilibrium?

S. Genheden and U. Ryde have analyzed conformational entropies of five protein and protein-ligand complexes with different methods for simulations up to 500 ns. They show that, for all cases, conformational entropies have not converged and that, therefore, all available states have not been reached.

Conformational entropies have been evaluated from the distribution of the dihedral angles, using different models: dihedral-distribution histogramming (DDH), von Mises approach (VMA), quasi-harmonic analysis (QHA), and normal-mode analysis (NMA). The latter was used in the estimation of ligand-protein binding free energies with the MM/GBSA method.

What is interesting in this article is that, whatever the entropy model used, no simulation converged and that entropies are still increasing at the end of the simulations. To explain this, the authors used a very simple model of protein containing only dihedral angles. In this case, the entropy of the model protein increases logarithmically with the simulation time, and the conformational entropy does not converge until the simulation time is larger than all the normal mode mean lifetimes (from 0.2 ps for 1 kJ/mol barrier to 12 h for 100 kJ/mol barrier). Using such an approach, the authors state that after 500 ns of simulation, most of their systems have sampled less than 70% of the conformational spaces and that the entropy will continue to increase with simulation time. Moreover, in the case of BPTI, after 1 ms of simulation, entropy has still not converged!

So, does this mean that we are all wrong when performing MD simulations? Will MD simulations ever reach equilibrium? In the strict sense, the answer is no: MD simulations do not converge, at least when regarding the entropy term. But, do we really need full convergence? As the authors say, reaching all available states for a protein would mean to fold and unfold the protein several times during the MD simulation. Do we (always) need this? In most cases, no.

Another interesting point is the MM/GBSA calculations. Using the NMA model to compute the entropy, the ligand-protein binding free energies converge in the 500 ns simulation time, showing a variation of less than a few kJ/mol. However, this is mainly due to error cancellation in the sum that defines the binding free energy in the MM/GBSA approach. In addition, the NMA approach produces much more stable estimates of the entropy than the other three methods (DDH, VMA, and QHA). This is due to the NMA approach that assumes a single conformation for the protein and estimates the entropy form the vibrational spectrum in this conformation. As long as the protein does not drastically change its conformation and its vibrational spectrum, the NMA entropy does not vary much (but then one could argue that this means that the NMA approach may not be very accurate).

In conclusion, I would say that this article shows that it is hopeless to see MD simulations of proteins to ever reach equilibrium (at least using a single trajectory). But that does not mean we should stop running MD simulations. We have to be (very) careful about the quantities that we are looking at. Different properties show varying sensitivity to this lack of strict equilibration.

Atomic-level simulations of current-voltage relationships in single-file ion channels

M.Ø. Jensen; V. Jogini; M. P. Eastwood and D.E. Shaw. J.Gen. Physiol, 141: 619-632 (2013)

Contributed by Ben Corry

There has been much discussion in these pages about papers assessing the accuracy of classical molecular dynamics in reproducing structural aspects of proteins, but less about whether such simulations can be used to understand physiological processes. Many such processes take place over time scales of ms to s and simulating them directly has long been beyond the scope of atomistic methods. But, the situation is rapidly changing with advances in computer hardware and software. One example of an important physiological process close to my heart is the conduction of ions through trans-membrane channels which underlies electrical signalling in nerve cells and takes place on a ms time scale. I am sure that many of us working in the field have thought that direct atomistic simulations have the potential to elucidate the physical mechanisms underlying this process, and have wondered how accurately such simulations could reproduce this phenomena. Yet again, D.E. Shaw Research provide us with an answer.

Making use of extensive computational resources and more than 1ms of simulation time, Jensen et al¹ measure the ionic current passing through a voltage gated potassium channel and the simpler gramicidin A channel under a range of voltages, allowing for a direct comparison to one of the most fundamental experimentally measureable properties. Sadly, the results are disappointing. Currents are about 40 times less and 300 times less than equivalent (highly accurate) experimental measurements in the potassium channel and gramicidin A respectively.

What are the reasons for this poor performance? Jensen et al point the finger at the most likely culprit, the accuracy of the non-polarisable biomolecular force field. Altering parameters such as the interaction strength between permeating ions and the protein has only a very small influence on the calculated current highlighting that simple modifications are unlikely to resolve the discrepancy between simulation and experiment. Deficiencies in the lipid model, such as the overestimation of the membrane dipolar potential, are also discussed; and while these are suggested to be a significant factor in the poor performance of the simulation they do not appear to be the major reason for the underestimation of ion currents. The final suggestion is that polarisable force fields may be required to accurately reproduce permeation rates under experimental conditions. Indeed, in the simple case of gA in which ions permeate one at a time, it would appear plausible that the inclusion of polarisability would improve the results by stabilising ions in the pore and reducing the barriers to permeation. It is not discussed is how much the structure of the proteins change during the simulations, especially under the influence of the electric field. If the structures of the proteins deviate from reality (again due to force field limitations) it is possible that this could also contribute to the poor performance of the simulations, in addition to problems with the ion-protein interactions and lack of polarisability. Given that it has only just become feasible to directly simulate ion currents with non polarisable force fields, it may be some time yet before we know if the use of polarisable ones will make the brute force simulation of physiological processes reliable.

References

1.       M.Ø. Jensen; V. Jogini; M. P. Eastwood and D.E. Shaw. J. Gen. Physiol, 141: 619-632