Diels–Alder Reactivities of Benzene, Pyridine, and Di-, Tri-, and Tetrazines: The Roles of Geometrical Distortions and Orbital Interactions

Yang, Y.-F.; Liang, Y.; Liu, F.; Houk, K. N. J. Am. Chem. Soc. 2016,138, 1660-1667
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

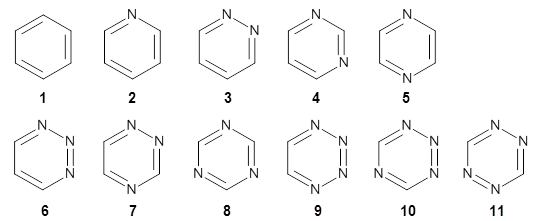
Houk has examined the Diels-Alder reaction involving ethene with benzene 1 and all of its aza-substituted isomers having four or fewer nitrogen atoms 2-11.¹ The reactions were computed at M06-2X/6-311+G(d,p).

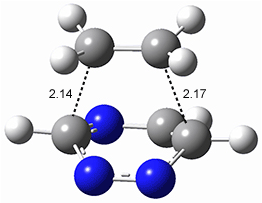
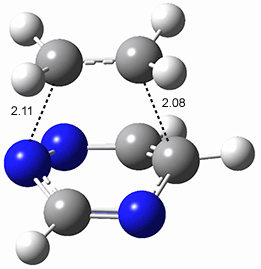
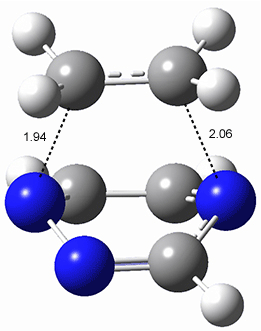
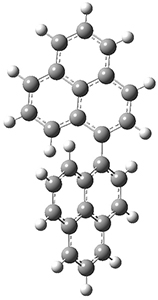
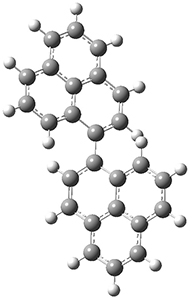
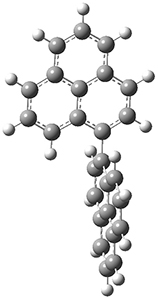
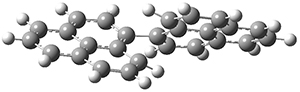
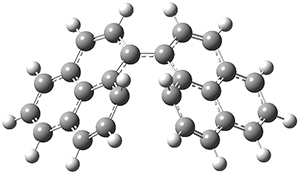
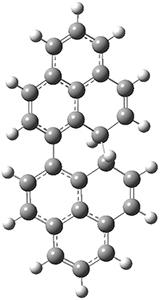
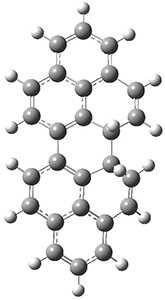
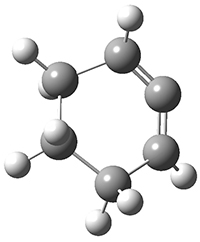
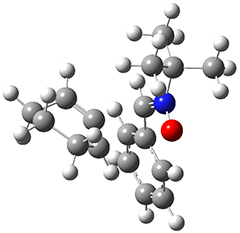
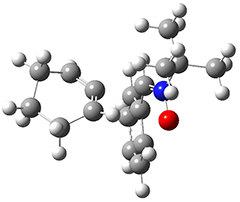
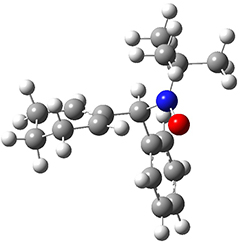
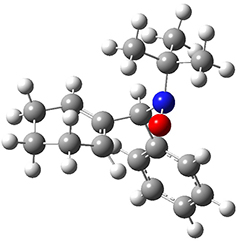
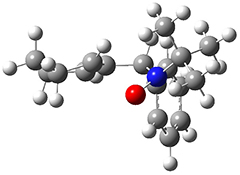
All of the possible Diels-Alder reactions were examined, and they can be classified in terms of whether two new C-C bonds are formed, one new C-C and one new C-N bond are formed, or two new C-N bonds are formed. Representative transition states of these three reaction types are shown in Figure 1, using the reaction of 7 with ethene.

Figure 1. M06-2X/6-311+G(d,p) optimized transition states for the Diels-Alders reactions of 7 with ethene.

A number of interesting trends are revealed. For a given type of reaction (as defined above), as more nitrogens are introduced into the ring, the activation energy decreases. Forming two C-C bonds has a lower barrier than forming a C-C and a C-N, which has a lower barrier than forming two C-N bonds. The activation barriers are linearly related to the aromaticity of the ring defined by either NICS(0) or aromatic stabilization energy, with the barrier decreasing with decreasing aromaticity. The barrier is also linearly related to the exothermicity of the reaction.

The activation barrier is also linearly related to the distortion energy. With increasing nitrogen substitution, the ring becomes less aromatic, and therefore more readily distorted from planarity to adopt the transition state structure.

References

(1) Yang, Y.-F.; Liang, Y.; Liu, F.; Houk, K. N. "Diels–Alder Reactivities of Benzene, Pyridine, and Di-, Tri-, and Tetrazines: The Roles of Geometrical Distortions and Orbital Interactions," J. Am. Chem. Soc. 2016,138, 1660-1667, DOI: 10.1021/jacs.5b12054.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Consistent structures and interactions by density functional theory with small atomic orbital basis sets

Stefan Grimme, Jan Gerit Brandenburg, Christoph Bannwarth, and Andreas Hansen (2015)
Contributed by Jan Jensen

B3LYP/6-31G* is still the de facto default level of theory for geometry optimizations of large-ish (ca 50-200 atoms) molecules and this paper introduces a cheaper, more accurate replacement called PBEh-3c. PBEh-3c is a basically PBE0/def2-SV(P) with added dispersion and BSSE corrections, where both functional and basis set has been modified slightly (for B-Ne in the case of the basis set).

As the authors write

Most striking is the roughly “MP2-quality” (or slightly better) obtained for the non-covalent complexes in the S22/S66 sets and equilibrium structures ($B_e$ values) for medium-sized organic molecules in the ROT34 set.

For example, the S22 and S66 geometries can be reproduced with an RMSD of 0.08 and 0.05 Å, respectively.  But this method is aimed at the entire periodic table and bond lengths between heavier atoms are also tested and well reproduced.

Though not specifically designed for it the method is also tested for intermolecular interaction energies, reaction energies, barrier heights.  Here PBEh-3c doesn't always outperform B3LYP/def2-SV(P) or M06-2X/def2-SV(P), but when it does it's typically a very significant improvement.  For example, the S30L (which includes host-guest complexes with multiple hydrogen bonds and/or charged systems) interaction energies are reproduced with an MAD of 3.4 kcal/mol, compared to 7.4 and 25.9 kcal/mol for M06-2X/def2-SV(P) and B3LYP/def2-SV(P), respectively.  3.3 kcal/mol may still sound like a lot but, for comparison, the corresponding MAD for PW6B95-D3/def2-QZVP(D) is 2.5 kcal/mol.

This work is licensed under a Creative Commons Attribution 4.0

Biphenalenylidene: Isolation and Characterization of the Reactive Intermediate on the Decomposition Pathway of Phenalenyl Radical

Uchida, K.; Ito, S.; Nakano, M.; Abe, M.; Kubo, T.  J. Am. Chem. Soc. 2016,138, 2399-2410

Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Uchida and co-workers reported on the preparation of biphenalenylidene 1 and its interesting electrocyclization to dihydroperopyrene 2.¹ The experimental barrier they find by experiment for the conversion of 1-Z to 1-E is only 4.3 kcal mol^-1. Secondly, the photochemical electrocyclization of 2-antito 1-Z proceeds rapidly, through an (expected) allowed conrotatory pathway. However, the reverse reaction did not occur photochemically, but rather did occur thermally, even though this is formally forbidden by the Woodward-Hoffman rules.

To address these issues, they performed a number of computations, with geometries optimized at UB3LYP(BS)/6-31G**. First, CASSCF computations indicated considerable singlet diradical character for 1-Z. Both 1-Z and 1-E show significant twisting about the central double bond, consistent with the inglet diradical character. 1-Z is 1.8 kcal mol^-1 lower in energy than 1-E, and the barrier for rotation interconverting these isomers is computed to be 7.0 kcal mol^-1, in reasonable agreement with the experiment. These geometries are shown in Figure 1.

1-Z	1-E
TS (Z→E)

Figure 1. UB3LYP(BS)/6-31G** optimized geometries of 1-Z and 1- and the transition state to interconvert these two isomers.

The conrotatory electrocyclization that takes 1-Z into 2-anti has a barrier of 26.0 kcal mol^-1 and is exothermic by 3.4 kcal mol^-1. The disrotatory process has a higher barrier (34.2 kcal mol^-1) and is endothermic by 8.4 kcal mol^-1. These transition states and products are shown in Figure 2. So, despite being orbital symmetry forbidden, the conrotatory path is preferred, and this agrees with their experiments.

TS (con)	TS (dis)
2-anti	2-syn

Figure 2. UB3LYP(BS)/6-31G** optimized geometries of 2-anti and 2-syn and the transition states leading to them.

The authors argue that the large diradical character of 1 leads to both its low Z→E rotational barrier, and the low barrer for electrocyclization. The Woodward-Hoffmann allowed disrotatory barrier is inhibited by its highly strained geometry, making the conrotatory path the favored route.

References

(1) Uchida, K.; Ito, S.; Nakano, M.; Abe, M.; Kubo, T. "Biphenalenylidene: Isolation and Characterization of the Reactive Intermediate on the Decomposition Pathway of Phenalenyl Radical," J. Am. Chem. Soc. 2016,138, 2399-2410, DOI: 10.1021/jacs.5b13033.

InChIs

1-E: InChI=1S/C26H16/c1-5-17-9-3-11-23-21(15-13-19(7-1)25(17)23)22-16-14-20-8-2-6-18-10-4-12-24(22)26(18)20/h1-16H/b22-21+
InChIKey=LOZZANITCNALJB-QURGRASLSA-N

1-Z: InChI=1S/C26H16/c1-5-17-9-3-11-23-21(15-13-19(7-1)25(17)23)22-16-14-20-8-2-6-18-10-4-12-24(22)26(18)20/h1-16H/b22-21-
InChIKey=LOZZANITCNALJB-DQRAZIAOSA-N

2-anti: InChI=1S/C26H18/c1-3-15-7-11-19-21-13-9-17-5-2-6-18-10-14-22(26(21)24(17)18)20-12-8-16(4-1)23(15)25(19)20/h1-14,19,21,25-26H/t19-,21-,25?,26?/m0/s1
InChIKey=BZIOOLOJBUBMSS-ATJINXRDSA-N

2-syn: InChI=1S/C26H18/c1-3-15-7-11-19-21-13-9-17-5-2-6-18-10-14-22(26(21)24(17)18)20-12-8-16(4-1)23(15)25(19)20/h1-14,19,21,25-26H/t19-,21+,25?,26?
InChIKey=BZIOOLOJBUBMSS-YXGNQKCYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Nitrone Cycloadditions of 1,2-Cyclohexadiene

Barber, J. S.; Styduhar, E. D.; Pham, H. V.; McMahon, T. C.; Houk, K. N.; Garg, N. K. J. Am. Chem. Soc. 2016, 138, 2512-2515
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

1,2-Cyclohexadiene 1 is a very strained and highly reactive species. Houk, Garg and co-workers report on its use as the ene component in a cyclization with a 1,3-dipole, namely nitrones.¹ For example, 1 reacts with nitrone 2 to give the cycloadducts 3a and 3b in a ratio of 8.9:1.

To investigate the mechanism of this reaction, they optimized the structures of all compounds at CPCM(acetonitrile)B3LYP/6-31G(d) and single-point energies were obtained using the B3LYP-D3 functional. The structures of some pertinent critical points are shown in Figure 1. They did locate a concerted transition state (TS1) leading to 3a, with a barrier of 14.5 kcal mol^-1, but could not find a concerted TS leading to 3b. (Also, the barriers leading to the other regioisomer are much higher than the ones leading to the observed products.) Rather, they identified a stepwise transition state (TS2) with a barrier of nearly the same energy (14.4 kcal mol^-1) that leads to the intermediate (INT), which lies 16.5 kcal mol^-1 below reactants. They located two transition states from his intermediate, TS3a and TS3b, leading to the two different products. The barrier to 3a is 1.2 kcal mol^-1 lower than the barrier leading to3b, and this corresponds nicely with the observed diastereoselectivity.

1 (0.0)
TS1 (14.5)	TS2 (14.4)
	INT (-16.5)
	TS3a (-7.4)	TS3b (-6.2)

Figure 1. CPCM(acetonitrile)B3LYP/6-31G(d) optimized geometries and CPCM(acetonitrile)B3LYP-D3/6-31G(d) free energies.

References

(1) Barber, J. S.; Styduhar, E. D.; Pham, H. V.; McMahon, T. C.; Houk, K. N.; Garg, N. K.
"Nitrone Cycloadditions of 1,2-Cyclohexadiene," J. Am. Chem. Soc. 2016, 138, 2512-2515, DOI:10.1021/jacs.5b13304.

InChIs

1: InChI=1S/C6H8/c1-2-4-6-5-3-1/h1,5H,2,4,6H2
InChIKey=NMGSDTSOSIPXTN-UHFFFAOYSA-N

2: InChI=1S/C11H15NO/c1-11(2,3)12(13)9-10-7-5-4-6-8-10/h4-9H,1-3H3/b12-9-
InChIKey=IYSYLWYGCWTJSG-XFXZXTDPSA-N

3a: InChI=1S/C17H23NO/c1-17(2,3)18-16(13-9-5-4-6-10-13)14-11-7-8-12-15(14)19-18/h4-6,9-11,15-16H,7-8,12H2,1-3H3/t15-,16-/m0/s1
InChIKey=HQIBSHJEOJPFTI-HOTGVXAUSA-N

3b: InChI=1S/C17H23NO/c1-17(2,3)18-16(13-9-5-4-6-10-13)14-11-7-8-12-15(14)19-18/h4-6,9-11,15-16H,7-8,12H2,1-3H3/t15-,16+/m1/s1
InChIkey=HQIBSHJEOJPFTI-CVEARBPZSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Reproducibility in density functional theory calculations of solids

Kurt Lejaeghere, Gustav Bihlmayer, Torbjörn Björkman, Peter Blaha, Stefan Blügel,Volker Blum, Damien Caliste, Ivano E. Castelli, Stewart J. Clark, Andrea Dal Corso,Stefano de Gironcoli, Thierry Deutsch, John Kay Dewhurst, Igor Di Marco, Claudia Draxl,Marcin Dułak, Olle Eriksson, José A. Flores-Livas, Kevin F. Garrity, Luigi Genovese,Paolo Giannozzi, Matteo Giantomassi, Stefan Goedecker, Xavier Gonze, Oscar Grånäs,E. K. U. Gross, Andris Gulans, François Gygi, D. R. Hamann, Phil J. Hasnip,N. A. W. Holzwarth, Diana Ius¸an, Dominik B. Jochym, François Jollet, Daniel Jones,Georg Kresse, Klaus Koepernik, Emine Küçükbenli, Yaroslav O. Kvashnin,Inka L. M. Locht, Sven Lubeck, Martijn Marsman, Nicola Marzari, Ulrike Nitzsche,Lars Nordström, Taisuke Ozaki, Lorenzo Paulatto, Chris J. Pickard, Ward Poelmans,Matt I. J. Probert, Keith Refson, Manuel Richter, Gian-Marco Rignanese, Santanu Saha,Matthias Scheffler, Martin Schlipf, Karlheinz Schwarz, Sangeeta Sharma,Francesca Tavazza, Patrik Thunström, Alexandre Tkatchenko, Marc Torrent,David Vanderbilt, Michiel J. van Setten, Veronique Van Speybroeck, John M. Wills,Jonathan R. Yates, Guo-Xu Zhang, Stefaan Cottenier Science 2016, 351, aad3000

Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission

A paper in Science (or equivalent journal) generally reports novel or ground-breaking research. At first sight, the paper I’ll discuss in this post[1] does not fit into that category: it reports an extensive set of tests on calculations for the equation of state (EOS) for 71 elemental solids using a variety of DFT codes, all using the PBE functional.

This paper is the product of a collaboration (you can find all the data, test suites etc on their web site[2]) that has been going for a while, and is both important and impressive. They have defined a single parameter, delta, which allows them to compare EOS calculated with different codes, giving a simple route to evaluating the reproducibility of DFT. This is immensely valuable, because different codes use different basis sets, different numerical solvers and different approaches to the external potential (full potential or a variety of pseudopotentials), and as a result will give different answers for the same simulation. The question is: how different are the answers ?

The key result from this paper is that modern DFT codes now achieve a precision[3] which is better than experimental; in terms of the paper, this means a delta value which is better than 1 meV/atom. This precision applies across various basis sets: plane waves, augmented plane waves, and numerical orbitals. It also applies to all-electron, PAW, and both ultra-soft and norm-conserving pseudopotential calculations. The summary table from the paper is reproduced below; the numbers given are the RMS value for delta across all 71 elements, while the colour indicates overall reliability.

Why is this work significant ? First, it gives a way to test new DFT codes and implementations, basis sets and approaches to the potential. So we now have an absolute reference against which codes can be compared. Second, it shows that there are now freely-available pseudopotential libraries which are precise in comparison to all-electron results (this is something that wasn’t true even five years ago - their Table 2, which shows the changing precision of different libraries over time, is fascinating). For both users and code developers, this is great news: there is no longer any question as to whether a particular pseudopotential is reliable, certainly within the context of single elements.

What could be added to the study ? Here are some ideas:

• More extensive tests. There are no tests of elements in different environments - and this can pose extreme challenges to pseudopotentials (think of the different oxidation states of transition metals, for instance).
• A comparison between the codes (e.g. speed, memory or parallelisation).
  This would be very challenging, but would be interesting data.
• More functionals and extensions of DFT will be important to include.

This paper is an immensely valuable contribution to the electronic structure community, as well as the wider scientific community, and it is good to see it published in a high-profile journal.

[1] DOI:10.1126/science.aad3000

[2] Delta value website from centre for molecular modelling

[3] Precision indicates the spread between different measured values, while accuracy indicates the deviation from the correct result (however “correct” is defined !) 

Coronene-Containing N-Heteroarenes: 13 Rings in a Row

Endres, A. H.; Schaffroth, M.; Paulus, F.; Reiss, H.; Wadepohl, H.; Rominger, F.; Krämer, R.; Bunz, U. H. F. J. Am. Chem. Soc. 2016, 138, 1792-1795
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Bunz and co-workers have synthesized the novel aromatic compound 1 that contains 13 acenes in a row.¹

They optimized the geometry of 1 at B3LYP/6-311G*, and its geometry is shown in Figure 1. Even though this compound has quite an extensive π-system, an unrestricted computations collapses to the closed-shell wavefunction.

1

Figure 1. B3LYP/6-311G* optimized geometry of 1. (As always, don’t forget to click on this image to launch JMol and visualize the molecule in 3-D.)

NICS(1)_πzz values for the rings are given in Table 1. Interestingly, the aromaticity of the coronene moiety is reduced; in fact the central ring (ring A, with rings labeled sequentially working towards either end from the center) has a very small NICS value of only -3.77.

Table 1. NICS(1)_πzz values for the rings of 1.

Ring	NICS(1)πzz
A B C D E F G H	-3.7 -12.2 -27.7 -28.7 -35.8 -36.1 -40.5 -29.8

References

(1) Endres, A. H.; Schaffroth, M.; Paulus, F.; Reiss, H.; Wadepohl, H.; Rominger, F.; Krämer, R.; Bunz, U. H. F. "Coronene-Containing N-Heteroarenes: 13 Rings in a Row," J. Am. Chem. Soc. 2016, 138, 1792-1795, DOI: 10.1021/jacs.5b12642.

InChIs

1: InChI=1S/C100H76N8O4Si4/c1-49(2)56-31-24-32-57(50(3)4)75(56)84-95(111)72-47-68-80-78-66(89-91(68)107-99-97(105-89)101-85-58(33-37-113(5,6)7)62-41-52-27-20-22-29-54(52)43-64(62)60(87(85)103-99)35-39-115(11,12)13)45-70-76-71(94(110)74(93(70)109)51-25-18-17-19-26-51)46-67-79(82(76)78)81-69(48-73(96(84)112)77(72)83(80)81)92-90(67)106-98-100(108-92)104-88-61(36-40-116(14,15)16)65-44-55-30-23-21-28-53(55)42-63(65)59(86(88)102-98)34-38-114(8,9)10/h17-32,41-50,74,84H,1-16H3
InChIKey=GNQHLGPUXJMSCH-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.