Cao, Y.; Liang, Y.; Zhang, L.; Osuna, S.; Hoyt, A.-L. M.; Briseno, A. L.; Houk, K. N. J. Am. Chem. Soc. 2014, 136, 10743-10751
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
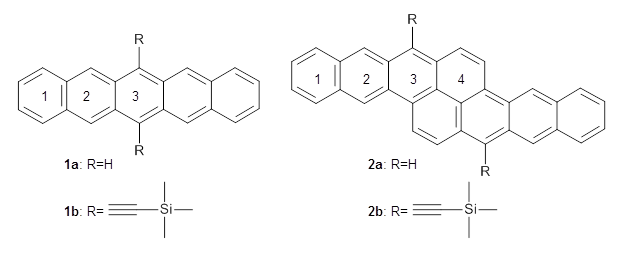
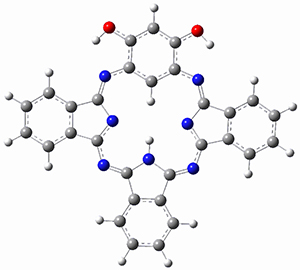
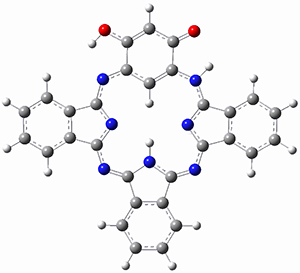
Pentacene and bistetracene ring numbering convention

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
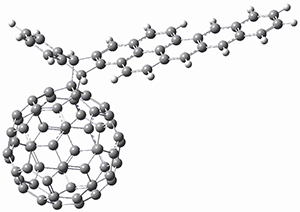
Diels-Alder reaction involving fullerenes have been known for some time. They occur across the [6,6] double bond of C60, the one between two fused 6-member rings. Houk and Briseno report on the Diels-Alder reaction of C60 with pentacene 1 and bistetracene 2 and compare their computations with experiments.1

Pentacene and bistetracene ring numbering convention
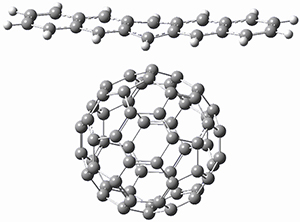
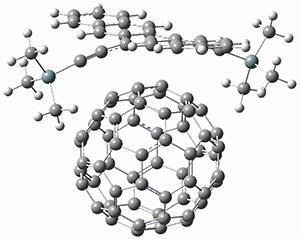
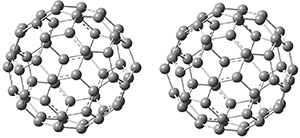
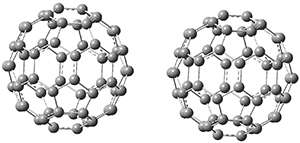
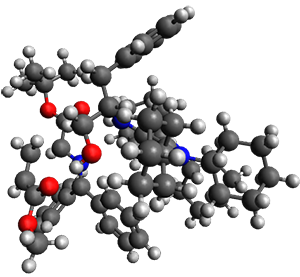
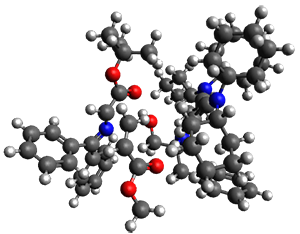
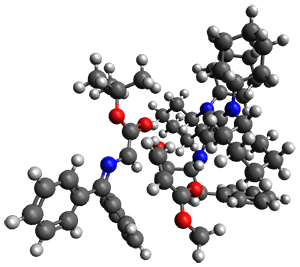
Computations were performed for the reaction of 1 and 2 with C60 at M06-2x/6-31G(d)//M062x-3-21G*. The reaction can occur with the dienophile being either ring 1, 2, or 3 of pentacene and ring 1, 2, 3, or 4 of bistetracene. They located TSs and products for all of these possibilities. Select TSs and products are shown in Figure 1.
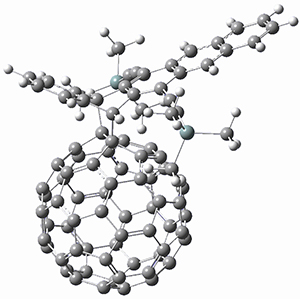
For the reaction of 1a, the lowest energy TS is for the reaction at the central ring (ring 3), and the resulting product is the lowest energy product. The transition state (PT_TS3) is shown in Figure 1. This TS has the least distortion energy of the three possibilities, because reacting at this central ring destroys the least amount of aromaticity of pentacene. For the reaction of 1b, the lowest barrier is again for reaction of ring 3 (through TMSPT_TS3). However, the product from the reaction with ring 2 (TMSPT_P2) is lower in free energy than TMSPT_P3, likely caused by steric interactions with the silyl substituents. This actually matches up with experiments which indicate that an analogue of TMSPT_P2 is the kinetic product butTMSPT_P3 is the thermodynamic product.
PT_TS3
| |
TMSPT_TS3
| |
TMSPT_P2
|
TMSPT_P3
|
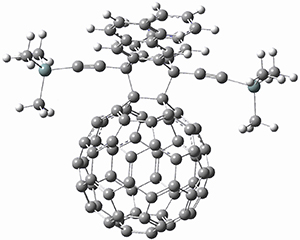
BT_TS2
|
BT_P2
|
Figure 1. M06-2x/3-21G* optimized geometries.
(Once again a reminder that clicking on any of these structures will launch JMol and you’ll be able to visualize and manipulate this structure in 3-D.)
(Once again a reminder that clicking on any of these structures will launch JMol and you’ll be able to visualize and manipulate this structure in 3-D.)
The computations involving the Diels-Alder reaction of C60 with either 2a or 2b come to the same conclusion. In both cases, the lowest barrier is for the reaction at ring 2, and the product of the reaction at this same ring is the only one that is endoergonic. The geometries of BT_TS2 and BT_P2 are shown in Figure 1. More importantly, the barrier for the Diels-Alder reaction involving 2a and 2b are at least 6 kcal mol-1 higher than the barriers for the reaction of 1a and 1b, in complete agreement with experiments that show little reaction involving analogues of 2b with C60, while analogues of 1b are reasonably rapid.
References
(1) Cao, Y.; Liang, Y.; Zhang, L.; Osuna, S.; Hoyt, A.-L. M.; Briseno, A. L.; Houk, K. N. "Why Bistetracenes Are Much Less Reactive Than Pentacenes in Diels–Alder Reactions with Fullerenes," J. Am. Chem. Soc.2014, 136, 10743-10751, DOI: 10.1021/ja505240e.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.