On the potentially transformative role of auxiliary-field quantum Monte Carlo in quantum chemistry: A highly accurate method for transition metals and beyond

James Shee, John L. Weber, David R. Reichman, Richard A. Friesner, and Shiwei Zhang (2022)
Highlighted by Jan Jensen

Figure 1 from this paper. (c) the authors

This paper highlights a big problem in the field of quantum chemistry and posits that a solution may be right around the corner. The problem is that we still can't routinely predict the thermochemistry of TM-containing compounds with the same degree of accuracy as we can for organic molecules. The main reason is that the former systems often have a high-degree of non-dynamic correlation which means that our CCSD(T) often does not give reliable results. We can model the non-dynamic correlation with CASSCF, but there is no good way to compute the dynamic correlation based on a CASSCF wavefunction. So when different DFT functional results give wildly different predictions for your TM-compound there is no way to tell which method, if any, if the best.

This paper argues that phaseless auxiliary-field quantum Monte Carlo (ph-AFQMC) may be the solution to this problem. ph-AFQMC represents the ground state as a stochastic linear combination of Slater determinants mapped as open-ended random walks starting from a trial wavefunction. The method accounts for both non-dynamic and dynamic correlation and the paper argues that chemical accuracy can be achieved with a few hundred random walks, which can be run in parallel and on GPUs.

So what's missing? According to the authors some of the improvements needed include: more efficient ways of reaching the CBS limit, more efficient random walks and a general, automatable protocol to generate optimal trial wave functions. Let's hope these improvements will be made soon, so we can explore a much larger portion of chemical space with confidence.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Quantum Chemical Data Generation as Fill-In for Reliability Enhancement of Machine-Learning Reaction and Retrosynthesis Planning

Alessandra Toniato, Jan P. Unsleber, Alain C. Vaucher, Thomas Weymuth, Daniel Probst, Teodoro Laino, and Markus Reiher (2022)
Highlighted by Jan Jensen

Part of Figure 7 from the paper. (c) The authors 2022. Reproduced under the CC BY NC ND 4.0 license

This is the first paper I have seen on combining automated QM-reaction prediction with ML-based retrosynthesis prediction. The idea itself is simple: for ML-predictions with low confidence (i.e. few examples in the training data) can automated QM-reaction prediction be used to check whether the proposed reaction is feasible, i.e. whether it is the reaction path with the lowest barrier?  If so, it could also be used to augment the training data.

The paper considers two examples using the Chemoton 2.0 method: one where the reaction is an elementary reaction and one where there are two steps (the Friedel-Crafts reaction shown above). It works pretty well for the former, but runs into problems for the latter.

One problem for non-elementary reactions is that one can't predict which atoms are chemically active from the overall reaction. Chemoton therefore must consider reactions involving all atom pairs and preferably more pairs of atoms simultaneously. The number of required calculations quickly gets out of hand and the authors conclude that "For such multistep reactions, new methods to identify the individual elementary steps will have to be developed to maintain the exploration within tight bounds, and hence, within reasonable computing time." 

However, even when they specify the two elementary steps for the Friedel-Crafts reaction, their method fails to find the second elementary step. The reason for this failure is not clear but could be due to the semiempirical xTB used for efficiency.

So the paper presents an interesting and important challenge to computational chemistry community. I wish more papers did this.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Semiempirical Hamiltonians learned from data can have accuracy comparable to Density Functional Theory

Frank Hu, Francis He, David J. Yaron (2022) 
Highlighted by Jan Jensen

Figure 7 from the paper. (c) The authors 2022. Reproduced under the BY-NC-ND licence

This paper uses ML techniques and algorithms (specifically PyTorch) to fit DFTB parameters, which results in a semiempirical quantum method (SQM) that has an accuracy similar to DFT. The advantage of such a physics-based method over a pure ML-based is that it is likely to be more transferable and requires much less training data. This should make it much easier to extend to other elements and new molecular properties, such as barriers.

Parameterising SQMs is notoriously difficult as the molecular properties depend exponentially on many of the parameters. As a result, most SQMs used today have parameterised by hand. The paper presents several methodological tricks to automate the fitting.

One is the use of high-order polynomial spline functions to describe how the Hamiltonian elements depend the fitting-parameters. The functions allow the computation of not only of the first derivative needed for back propagation, but also high-order derivatives, which are used for regularisation to avoid overfitting and keeping the parameters physically reasonable. Finally, the SCF and training loops are inverted to that the he charge fluctuations needed for the Fock operator are updated based on the current model parameters every 10 epochs. This enables computationally efficient back propagation during training, which is important because the training set is on the order of 100k.

Another neat feature is that the final model is simply a parameter file (SKF file), which can be read by most DFTB programs. So there is nothing new for the user to implement. However, currently the implementation is only for CNHO.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Active Learning for Small Molecule pKa Regression; a Long Way To Go

Paul G. Francoeur, Daniel Peñaherrera, and David R. Koes (2022)
Highlighted by Jan Jensen

Parts of Figures 5 and 6. (c) The authors 2022. Reproduced under the CC-BY licence

One approach to active learning is to grow the training set with molecules for which the current model has the highest uncertainties. However,  according to this study, this approach does not seem to work for small-molecule pKa prediction where active learning and random selection give the same results (within the relatively high standard deviations) for three different uncertainty estimated. 

The authors show that there are molecules in the pool that can increase the  initial accuracy drastically, but that the uncertainties don't seem to help identify these molecules. The green curve above is obtained by exhaustively training a new model for every molecule in the pool during each step of the active learning  loop and selecting the molecule that gives the largest increase in accuracy for the test set. Note that the accuracy decreases towards the end meaning that including some molecules in the training set diminishes the performance.

The authors offer the following explanation for their observations: "We propose that the reason active  learning failed in this pKa prediction task is that all of the molecules are informative."

That's certainly not hard to imagine given the is the small size of the initial training set (50). It would have been very instructive to see the distribution of uncertainties for the initial models. Does every molecule have roughly the same (high) uncertainty? If so, the uncertainties would indeed not be informative. 

Also, uncertainties only correlate with (random) errors on average. The authors did try adding molecules in batches, but the batch size was only 10. 

It would have been interesting to see the performance if one used the actual error, rather than the uncertainties, to select molecules. That would test the case where uncertainties correlate perfectly with the errors.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Is there evidence for exponential quantum advantage in quantum chemistry?

Seunghoon Lee, Joonho Lee, Huanchen Zhai, Yu Tong, Alexander M. Dalzell, Ashutosh Kumar, Phillip Helms, Johnnie Gray, Zhi-Hao Cui, Wenyuan Liu, Michael Kastoryano, Ryan Babbush, John Preskill, David R. Reichman, Earl T. Campbell, Edward F. Valeev, Lin Lin, Garnet Kin-Lic Chan (2022)
Highlighted by Jan Jensen

Figure 1 from the paper. (c) 2022 the authors. Reproduced under the CC-BY licence.

Quantum chemical calculations are widely seen as one of quantum computings killer app's. This paper examines the available evidence for this assertion and doesn't find any. 

The potential of quantum computing rests on two assumptions: that the cost of quantum computer calculations on chemical systems scales polynomially with system size, while the corresponding calculations on classical computers scale exponentially. 

The former assumption is true for the actual quantum "computation" and the latter assertion is true for the Full CI solution. However, this paper suggests that preparing the state for the quantum "computation" may scale exponentially with system size, and that we don't need Full CI accuracy and that chemically accurate methods such as coupled-cluster based method scale polynomially with system size for a given desired accuracy.

The argument for the potential exponential scaling for system preparation is as follows: If you want the energy of the ground state you have to provide a guess at the ground state wavefunction that resembles the exact wavefunction as much as possible. More precisely, the probability of obtaining the ground state energy scales as $S^{-2}$, where S is the overlap between the trial and exact wavefunction. The authors show that $S$  scales exponentially with system size for a series of Fe-S clusters, which suggests an overall exponential dependence for the quantum computations.

The argument for polynomial scaling of chemically accurate quantum chemistry calculations has two parts: "normal" organic molecules and strongly correlated systems. 

The former is pretty straight-forward: no one knowledgeable is really arguing that CCSD(T)-level accuracy is insufficient for ligand-protein binding energies and CCSD(T) scales polynomially with system size. So the simple notion of accelerating drug discovery by computing this with quantum computers does not hold water.

However, CCSD(T) does not work for strongly correlated systems and we don't have any real practical alternative for which we can test the scaling. Instead the authors look at simpler model of strongly correlated systems and demonstrate polynomial scaling with system size.  

As the authors are carefull to point out, none of this represents a rigorous proof of anything. But it is far from obvious that quantum chemistry is the killer app for quantum computing that most people seem to think it is. 

In addition to the paper you can find a very clear lecture on the topic here.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Sample Efficiency Matters: A Benchmark for Practical Molecular Optimization

Wenhao Gao, Tianfan Fu, Jimeng Sun, Connor W. Coley (2022)
Highlighted by Jan Jensen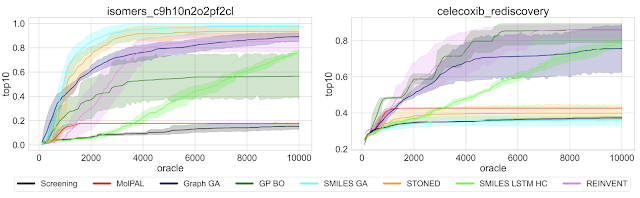

Figure 1 from the paper. (c) The authors 2022. Reproduced under the CC-BY license.

The development of generative models that can find molecules with certain properties has become very popular but there are very few studies that compare them, so it's hard to know what works best. This study compares the performance of 25 different generative models in 23 different optimisation tasks and draws some very interesting conclusions.

None of these methods find the optimum value given an "budget" of 10,000 oracle evaluations and for some tasks the best performance is not exactly impressive. This doesn't bode well for some real life applications where even a few hundred property evaluations are challenging. 

Some methods are slower to converge than others, so you might draw completely different conclusions regarding efficiency if you 100,000 oracle evaluations. Similarly, some methods have high variability in performance so you might draw very different conclusions from 1 run compared to 10 runs. This is especially a consideration for problems when you can only afford one run. It might be better to choose a method that performs slightly worse on average but is less variable, rather than risk a bad run from a highly variable method that performs better on average.

The method that performed best overall is one of the oldest methods, published in 2017! 

Food for thought

This work is licensed under a Creative Commons Attribution 4.0 International License.

Deep Learning Metal Complex Properties with Natural Quantum Graphs

Hannes Kneiding, Ruslan Lukin, David Balcells (2022)
Highlighted by Jan Jensen

Figure 2 from the paper (c) The authors. Reproduced under the CC-BY-NC-ND 4.0 license

While there's been a huge amount of ML work on organic molecules, there as been comparatively little on trantition metal complexes (TMCs). One of the reasons is that many of the cheminformatics tools we take for granted are harder to apply to TMCs due to their more complex bonding situations. This makes bond perception and computing node-features like formal atomic charges, and hence graph representations, quite tricky. Which, in turn, makes standard ML tools like binary finger prints or graph-convolution NNs tricky to apply to TMCs.

This paper suggest using data from DFT/NBO calculations to create so-called "quantum graphs", where the edges are determined using both bonding orbitals and bond-orders while node- and edge-features are derived from other NBO properties.

This representation is combined with two graph-NN methods (MPNN and MXMNet) and trained against DFT properties such as the HOMO-LUMO gap. The results are quite good and generally better than radius graph methods such as SchNet. However, one should keep in mind that both the descriptors and properties are computed with DFT.

Given that the computational cost of the descriptors is basically the same as the property of interest, this is a proof-of-concept paper that shows the utility of the general idea. However, it remains to be seen whether cheaper descriptors (e.g. based on semi-empirical calculations) result in similar performance. However, given the current sparcity of ML tools for TMCs this is a very welcome advance.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Computer-designed repurposing of chemical wastes into drugs

Agnieszka Wołos, Dominik Koszelewski, Rafał Roszak, Sara Szymkuć, Martyna Moskal, Ryszard Ostaszewski, Brenden T. Herrera, Josef M. Maier, Gordon Brezicki, Jonathon Samuel, Justin A. M. Lummiss, D. Tyler McQuade, Luke Rogers & Bartosz A. Grzybowski (2022)
Highlighted by Jan Jensen

Figure 2a from the paper. (c) 2022 the authors

When I talk to people about retrosynthesis prediction the often mention that synthetic chemists don't tend to use them. There are many reasons for that including various shortcomings of the suggested routes but also the fact that, from a time saving perspective, the retrosynthesis planning makes up a small part of the synthesis process. One common answer to this is "OK, but wait til the robots arrive", but there are several important applications that are applicable right now. 

For example, on my own research in de novo molecule discovery I'm often left with hundreds of promising molecules where the only remaining selection criterion is ease of synthesis. Here I routinely use retrosynthesis programs to rank the molecules in terms of number of synthesis steps to make the shortlist of 10-20 molecules that can be presented to experimental collaborators. 

This paper presents another example of science that would be impossible without these computational tools. The authors search for reaction networks that connect 189 small molecule waste by-products from chemical industry to 4113 high-value molecules (approved drugs and agrochemicals). The use a reaction prediction algorithm called Allchemy to iteratively generate increasingly complicated molecules and, at each step, bias the search towards the target. Among the 300 million molecules that result from this process the were able to identify 167 target molecules, with an average of 216 synthetic paths per target. The synthetic paths are further ranked using a complicated scoring functions that accounts for all sorts of practical considerations, since aim is to produce large quantities of each target, and a few of the paths are experimentally verified on the kg scale.

One interesting part the approach is the prediction of reaction conditions, which is done in terms of categories: e.g. protic/aprotic and polar/nonpolar solvents, and very low, low, room temperature, high, and very high temperatures. This makes a lot more sense to than trying to predict the exact solvent or temperature.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Pairwise Difference Regression: A Machine Learning Meta-algorithm for Improved Prediction and Uncertainty Quantification in Chemical Search

Michael Tynes, Wenhao Gao, Daniel J. Burrill, Enrique R. Batista, Danny Perez, Ping Yang, and Nicholas Lubbers (2021)
Highlighted by Jan Jensen

TOC picture from the paper (c) 2021 ACS

This paper tries to solve two problems at once: data augmentation for small data sets and a method-independent uncertainty quantification (UQ). 

Data augmentation is quite common in areas like image classification where images can be perturbed (e.g. rotated by a few degrees) and still be recognisable. However, this is difficult in chemistry where small perturbations in structure can have a non-negligible effect on properties. For text-based molecular representation once can use non-canonical smiles for augmentation, but there is no generally applicable method.

Similarly, most UQ methods are specific to the machine learning model-type, with the exception of ensemble methods that requires the training and deployment of several models, which can be expensive.

The paper offers a simple solution to both. The method is trained to reproduce the ground truth difference for all $n^2$ molecule pairs thereby increasing the training set size significantly. When making a prediction for a new molecule, the model predicts the differences relative to all training set molecules with the standard deviation serving as a measure of prediction uncertainty. Pretty neat idea and easy to implement! The main change is to construct molecular representations for the molecule pairs but the authors outline one easy-to-implement approach.

Depending on the task and training set size the data augmentation decreases the MAE by 3-40%. UQ quality is notoriously difficult to quantify, but the method appears to give uncertainties similar to those obtained by a random forest method.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Machine Learning May Sometimes Simply Capture Literature Popularity Trends: A Case Study of Heterocyclic Suzuki−Miyaura Coupling

Wiktor Beker, RafałRoszak, Agnieszka Wołos, Nicholas H. Angello, Vandana Rathore, Martin D. Burke, and Bartosz A. Grzybowski (2022)
Highlighted by Jan Jensen

What do you infer from this quote from the paper (emphasis added)?

Another important problem, tackled herein, deals with the prediction of optimal conditions for a particular reaction in which there are generally multiple viable choices of solvents or reagents. Several works[21−24] have attempted to use ML for the prediction of reaction conditions, and the overall message they seem to convey is that ML can, in fact, offer accurate predictions provided adequate numbers of literature examples on which to build the models (but see also critical ref 6). However, here, we demonstrate with a case study that this may have been an overoptimistic interpretation, and that even with large quantities of carefully curated literature data, ML approaches may not perform considerably better than estimates based on the popularity of reaction conditions reported in the literature. In other words, these ML models do not provide significantly more insights than just suggesting the most popular conditions which could be obtained by simple statistics over literature examples[25,26] and no “machine intelligence.”

I can tell you what I inferred. References 21-24 used ML models to predict optimal reaction conditions, but failed to check whether they "provide significantly more insights than just suggesting the most popular conditions". I also inferred that the results from this study suggests that, had the authors checked, they would have found that not to be the case. 

However, the four references refer to two papers (21 and 23) by Doyle and co-workers on the prediction of reaction yields (not conditions) and two papers, one by Coley and co-workers and one by Reisman and co-workers (22 and 24, respectively), on the prediction of reaction conditions with comparison to popularity baselines. 

The paper looks at the prediction of solvent and base (and not catalysts and temperature as implied by the TOC graphic above) for ca 10,000 Suzuki coupling reactions from Reaxys. The best top-1 accuracy for base and solvent for ML are 80.6% and 51.7%, compared to popularity baseline values of 76.8% and 29.8%. The authors use the term "significantly" (and related terms) without ever quantifying what they deem significant, but to me the ML solvent predictions seem significantly better than the popularity baseline. 

Furthermore, as Coley and co-workers point out the true metric is the accuracy of the combined prediction, e.g. correct solvent and base. For example, in the case of correct catalysts and solvent and reagent Coley and co-workers found an accuracy of 57.3% compared to a popularity baseline of only 5.7%. However, I am not even certain whether Grzybowski and co-workers would deem that a significant improvement.

On a more constructive note, the topic of the paper does relate to an interesting fundamental question in ML on how to deal with imbalances data, i.e. where there is a a very popular single choice. One would perhaps naively suspect that this would be easier for a machine to learn, i.e. you just have to learn a few exceptions. But how to you typically learn exceptions? By memorising them, and we tend to employ many ML techniques to avoid just this.  

This work is licensed under a Creative Commons Attribution 4.0 International License.

Findings hits among billions of molecules

Assaf Alon, Jiankun Lyu, Joao M. Braz, Tia A. Tummino, Veronica Craik, Matthew J. O’Meara, Chase M. Webb, Dmytro S. Radchenko, Yurii S. Moroz, Xi-Ping Huang, Yongfeng Liu, Bryan L. Roth, John J. Irwin, Allan I. Basbaum, Brian K. Shoichet & Andrew C. Kruse. Structures of the σ2 receptor enable docking for bioactive ligand discovery (2021)

Arman A. Sadybekov, Anastasiia V. Sadybekov, Yongfeng Liu, Christos Iliopoulos-Tsoutsouvas, Xi-Ping Huang, Julie Pickett, Blake Houser, Nilkanth Patel, Ngan K. Tran, Fei Tong, Nikolai Zvonok, Manish K. Jain, Olena Savych, Dmytro S. Radchenko, Spyros P. Nikas, Nicos A. Petasis, Yurii S. Moroz, Bryan L. Roth, Alexandros Makriyannis & Vsevolod Katritch Synthon-based ligand discovery in virtual libraries of over 11 billion compounds (2021)

Highlighted by Jan Jensen

Figure 2a and b from Alon et al. (c) 2021 Nature

The recent developments in make-on-demand molecular libraries present an interesting methodological challenge to virtual screening. Not too long ago, such a library would have hundreds of millions and even 1 billion molecules and there was still a chance to dock a significant portion of these libraries. However, the sizes of the libraries have grown to well beyond 20 billion and show no sign of stopping. There is no way wholesale docking can keep up with this growth so new approaches are needed. 

One computational approach that has kept up with the growth of make-on-demand libraries is similarity searching. It is still possible to search these enormous libraries for similar molecules in just a few minutes. 

Alon et al. uses this general idea to select and dock 490 million molecules with properties that are similar to known binders to the target. Based on the docking scores they prioritised 577 molecules of which 484 were successfully made and 127 showed good activity against the target. 20,000 analogues of the four best candidates are then extracted from among 28 billion molecules in the Enamine REAL Space make-on-demand library, and docked. The 105 best candidates were made and tested leading to further improvement in the measured affinities.

Sadybekov et al. essentially docks the individual building blocks used in the make-on-demand library and then combined the best-scoring fragments into about 1 million molecules for a second round of docking. Using this approach they identified 80 promising candidates of which 60 could be synthesised. Of these 60 molecules, 21 proved active. 920 analogues of the three best candidates are then extracted from among 11 billion molecules in the Enamine REAL Space make-on-demand library, and docked. The 121 best candidates were made and tested leading to further improvement in the measured affinities.

There are several take home messages here. 

The percentage of active compounds against a particular target in library is very small, so you don't get a lot of useful hits until you work with these enormous libraries.

Docking does help in identifying active compounds. Docking has a bad rep in certain circles and I have seen several people refer to them as "random number generators" but studies like these show that this is not the case. Sure, if one expects an excellent, or even respectable, correlation coefficient between docking scores and binding affinities, one will be sorely disappointed.  However, as these studies show, molecules with good docking scores have a much higher chance at being active than molecules with bad docking scores. 

The success rate seems to be about 30-50% depending on the target. So if you are in the lower end and only able to make and test a handful of candidates (which is often the case for academic studies), there's a reasonable chance you won't find any actives and conclude that docking is useless. It's only when you are able to make and test dozens of molecules that you see that docking is working for you. The make-on-demand libraries now makes such numbers feasible for academics.

Finally, several of the co-authors on the two papers I highlight are Ukrainian and are, along with their families and friends, likely in grave danger right now as their country is being attacked by Putin and his ilk. 

This work is licensed under a Creative Commons Attribution 4.0 International License.

Machine learning potentials always extrapolate, it does not matter.

Claudio Zeni, Andrea Anelli, Aldo Glielmo, and Kevin Rossi (2021)
Highlighted by Jan Jensen

The Convex Hull (blue line) encloses the blue points. It maximises the area while minimising the circumference.

ML models are generally thought to only interpolate, but this paper suggests that this is not the case. On first sight this seems counterintuitive but on some reflection this may not be so strange at all.

First of all, the authors define an extrapolation as a prediction for a point outside (red point) the Convex Hull (blue line) defined by the training set points (blue points). They perform this analysis for three train/test sets related to solid state chemistry and show that between 80% and 100% of the test sets data points lie outside the Convex Hull defined by the training set data points, but ML models trained on the training set perform satisfactorily for the test set (hence the title).

While this might seem counterintuitive at first, is it really so strange that a model trained on the blue points performs better for the red point than the green point?  The red point is closer to the the blue points and there is really only extrapolation in the x direction. 

The representation vectors used in this study all have at least 100 dimensions and a point is said to correspond to an extrapolation if it lies outside the Convex Hull in only one of these dimensions. By using PCA the authors show that in some cases extrapolation occurs for all test points when considering only the 10 most important dimensions, while 20 dimensions are needed for truly accurate results. However, for most cases reasonable accuracy can be obtained with 4 dimensions, where more than 90% of the test set is contained in the Convex Hull of the training set. So IMO the picture is not as clear cut as the title suggests.

The authors show that the best predictor of accuracy is the density of training set points in the region of the test set molecule.

This work is licensed under a Creative Commons Attribution 4.0 International License.