Planning chemical syntheses with deep neural networks and symbolic AI

Marwin H. S. Segler, Mike Preuss, Mark P. Waller (2018)
Highlighted by Jan Jensen

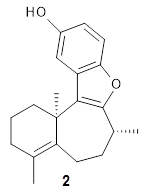
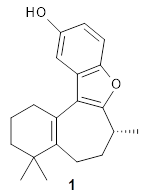
Figure 1 from the paper. Copyright 2018 Springer Nature

The paper uses a Monte Carlo tree search (MCTS) algorithm (also used in AlphaGo Zero) to suggest retrosynthetic routes that were just as good as those proposed by expert organic chemist. Remarkably the underlying "expert knowledge" is automatically extracted from reaction databases into three neural networks. Thus, the method is referred to as 3N-MCTS.

At the core of this approach are two neural networks that can predict the probability of a molecule undergoing one of either 301,671 or 17,134 chemical transformations, the latter being more computationally efficient than the former. The networks were trained on tranformation rules from 12.4 million single-step reactions from the Reaxys chemistry database, i.e. determined automatically without human intervention.

  

The retrosynthetic "game" is won if the target molecule can be completely decomposed into predefined precursor molecules within 25 retrosynthetic steps, where the 50 most probable chemical transformations are considered for each step. It is not practically possible to test all $50^{25} \approx 10^{40}$ possible retrosynthetic paths so a MCTS is used to search for the best path.

A MCTS starts by evaluating a number of paths randomly and then assigning likelihood scores to the early parts of the paths depending on whether the paths lead to winners or not. The process is then repeated except that the early steps in the path are chosen based on likelihood scores, which are continuously updated and added to unscored steps.  The changing likelihood scores means that the search for new paths is directed towards the more promising areas of the path tree. I have given a short illustration of the process here. The process is repeated for a given number of steps and the path with the best set of likelihood scores is selected.

One of the tests of the method was a double blind study where experienced synthetic chemists were asked to choose between retrosynthetic routes developed by experts and by 3N-MCTS. The study found no clear preference!

I couldn't find any information about code availability.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Beyond optical rotation: what’s left is not always right in total synthesis

Joyce, L. A.; Nawrat, C. C.; Sherer, E. C.; Biba, M.; Brunskill, A.; Martin, G. E.; Cohen, R. D.; Davies, I. W., Chem. Sci. 2018, 9, 415
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

The structure of (+)-frondosin B 1 has been the subject of some concern. The compound has been synthesized by a number of research groups with the expected R isomer as the target. However, the Danishefsky¹ and MacMillan² synthesis led to a molecule with [α]_D of about +16°, while Trauner³ reports a value of -16.8° and Ovaska⁴ prepared the S isomer with [α]_D = -17.3°. Something is amiss here.

Joyce and coworkers have looked into this structure problem through a combination of advanced analytical techniques and computational chemistry.⁵ They utilize optical activity, electronic circular dichroism (ECD) and vibrational circular dichroism (VCD) and compare the experiments with computational results. IR and VCD were computed at B3LYP/6-31G** using a Boltzmann-weighted set of low-energy conformations. ECD computations were done at CAM-B3LYP/6-31++G**//B3LYP/6-31G**.

Basically, they found that (+)-frondosin B does have the R stereocenter. The different synthetic schemes did actually all lead to the same isomer, tested by looking at key intermediates along the way. The discrepancy in the optical activity is due to a small impurity, 2, that has the opposite rotation and a magnitude 10 times greater than that of authentic 1.

This paper is another nice example demonstrating the power of modern computational approaches to spectra that can be extremely valuable in structure determination. Organic chemists of all stripes should certainly be aware of how this tool can complement experiments.

My thanks to Derek Lowe who posted on this paper in his In The Pipeline blog.

References

1) Inoue, M.; Carson, M. W.; Frontier, A. J.; Danishefsky, S. J., "Total Synthesis and Determination of the Absolute Configuration of Frondosin B." J. Am. Chem. Soc.
2001, 123, 1878-1889, DOI: 10.1021/ja0021060.

2) Reiter, M.; Torssell, S.; Lee, S.; MacMillan, D. W. C., "The organocatalytic three-step total synthesis of (+)-frondosin B." Chem. Sci. 2010, 1, 37-42, DOI: 10.1039/C0SC00204F.

3) Hughes, C. C.; Trauner, D., "Palladium-catalyzed couplings to nucleophilic heteroarenes: the total synthesis of (−)-frondosin B." Tetrahedron 2004, 60, 9675-9686, DOI: 10.1016/j.tet.2004.07.041.

4) Ovaska, T. V.; Sullivan, J. A.; Ovaska, S. I.; Winegrad, J. B.; Fair, J. D., "Asymmetric Synthesis of Seven-Membered Carbocyclic Rings via a Sequential Oxyanionic 5-Exo-Dig Cyclization/Claisen Rearrangement Process. Total Synthesis of (−)-Frondosin B." Org. Letters 2009, 11, 2715-2718, DOI: 10.1021/ol900967j.

5) Joyce, L. A.; Nawrat, C. C.; Sherer, E. C.; Biba, M.; Brunskill, A.; Martin, G. E.; Cohen, R. D.; Davies, I. W., "Beyond optical rotation: what’s left is not always right in total synthesis." Chem. Sci. 2018, 9, 415-424, DOI: 10.1039/C7SC04249C.

InChIs

1: InChI=1S/C20H24O2/c1-12-6-8-16-14(5-4-10-20(16,2)3)18-15-11-13(21)7-9-17(15)22-19(12)18/h7,9,11-12,21H,4-6,8,10H2,1-3H3/t12-/m1/s1
InChIKey=LSPMJSWSYGOLFD-GFCCVEGCSA-N

2: InChI=1S/C20H24O2/c1-12-5-4-10-20(3)16(12)8-6-13(2)19-18(20)15-11-14(21)7-9-17(15)22-19/h7,9,11,13,21H,4-6,8,10H2,1-3H3/t13-,20-/m1/s1
InChIKey=ZBXZDKMLFIJFHG-ZUOKHONESA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

DeePCG: A Deep Neural Network Molecular Force Field

DeePCG: constructing coarse-grained models via deep neural networks. L Zhang, J Han, H Wang, R Car, Weinan E. arXiv:1802.08549v2 [physics.chem-ph]
Contributed by Jesper Madsen

The idea of “learning” a molecular force field (FF) using neural networks can be traced back to Blank et al. in 1995.[1] Modern variations (reviewed recently by Behler[2]), such as the DeePCG scheme[3] that I highlight here, seem to have two key innovations to set them apart from earlier work: network depth and atomic environment descriptors. The latter was the topic of my recent highlight and Zhang et al.[3] take advantage of similar ideas.

Figure 1: “Schematic plot of the neural network input for the environment of CG particle i, using water as an example. Red and white balls represent the oxygen and the hydrogen atoms of the microscopic system, respectively. Purple balls denote CG particles, which, in our example, are centered at the positions of the oxygens.)” from ref. [3]    

Zhang et al. simulate liquid water using ab initio molecular dynamics (AIMD) on the DFT/PBE0 level of theory in order to train a coarse-grained (CG) molecular water model. The training is done by a standard protocol used in CGing where mean forces are fitted by minimizing a loss-function (the natural choice is the residual sum of squares) over the sampled configurations. CGing liquid water is difficult because of the necessity of many-body contributions to interactions, especially so upon integrating out degrees-of-freedom. One would therefore expect that a FF capable of capturing such many-body effects to perform well, just as DeePCG does, and I think this is a very nice example of exactly how much can be gained by using faithful representations of atomic neighborhoods instead of radially symmetric pair potentials. Recall that traditional force-matching, while provably exact in the limit of the complete many-body expansion,[4] still shows non-negligible deviations from the target distributions for most simple liquids when standard approximations are used.

FF transferability, however, is likely where the current grand challenge is to be found. Zhang et al. remark that it would be convenient to have an accurate yet cheap (e.g., CG) model for describing phase transitions in water. They do not attempt this in the current preprint paper, but I suspect that it is not *that* easy to make a decent CG model that can correctly get subtle long-range correlations right at various densities, let alone different phases of water and ice, coexistences, interfaces, impurities (non-water moieties), etc. Machine-learnt potentials continuously demonstrate excellent accuracy over the parameterization space of states or configurations, but for transferability and extrapolations, we are still waiting to see how far they can get.

References

[1] Neural network models of potential energy surfaces. TB Blank, SD Brown, AW Calhoun, DJ Doren. J Chem Phys 103, 4129 (1995)

[2] Perspective: Machine learning potentials for atomistic simulations. J Behler. J Chem Phys 145, 170901 (2016)

[3] DeePCG: constructing coarse-grained models via deep neural networks. L Zhang, J Han, H Wang, R Car, Weinan E. arXiv:1802.08549v2 [physics.chem-ph]

[4] The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. WG Noid, J-W Chu, GS Ayton, V Krishna, S Izvekov, GA Voth, A Das, HC Andersen. J Chem Phys 128, 244114 (2008)

Comprehensive theoretical study of all 1812 C60 isomers

Sure, R.; Hansen, A.; Schwerdtfeger, P.; Grimme, S., Phys. Chem. Chem. Phys. 2017, 19, 14296
Contributed by Steven Bacharach

Reposted from Computational Organic Chemistry with permission

The Grimme group has examined all 1812 C₆₀ isomers, in part to benchmark some computational methods.¹ They computed all of these structures at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP. The lowest energy structure is the expected fullerene 1 and the highest energy structure is the nanorod 2 (see Figure 1).

1

2

Figure 1. Optimized structures of the lowest (1) and highest (2) energy C₆₀ isomers.

About 70% of the isomers like in the range of 150-250 kcal mol^-1 above the fullerene 1, and the highest energy isomer 2 lies 549.1 kcal mol^-1 above 1. To benchmark some computational methods, they selected the five lowest energy isomers and five other isomers with higher energy to serve as a new database (C60ISO), with energies computed at DLPNO-CCSD(T)/CBS*. The mean absolute deviation of the PBE-D3/def2-TZVP relative energies with the DLPNO-CCSD(T)/CBS* energies is relative large 10.7 kcal mol^-1. However, the PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP method is considerably better, with a MAD of only 1.7 kcal mol^-1. This is clearly a reasonable compromise method for fullerene-like systems, balancing accuracy with computational time.

They also compared the relative energies of all 1812 isomers computed at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP with a number of semi-empirical methods. The best results are with the DFTB-D3 method, with an MAD of 5.3 kcal mol^-1.

References

1) Sure, R.; Hansen, A.; Schwerdtfeger, P.; Grimme, S., "Comprehensive theoretical study of all 1812 C₆₀isomers." Phys. Chem. Chem. Phys. 2017, 19, 14296-14305, DOI: 10.1039/C7CP00735C.

InChIs

1: InChI=1S/C60/c1-2-5-6-3(1)8-12-10-4(1)9-11-7(2)17-21-13(5)23-24-14(6)22-18(8)28-20(12)30-26-16(10)15(9)25-29-19(11)27(17)37-41-31(21)33(23)43-44-34(24)32(22)42-38(28)48-40(30)46-36(26)35(25)45-39(29)47(37)55-49(41)51(43)57-52(44)50(42)56(48)59-54(46)53(45)58(55)60(57)59
InChIKey=XMWRBQBLMFGWIX-UHFFFAOYSA-N

2: InChI=1S/C60/c1-11-12-2-21(1)31-41-32-22(1)3-13(11)15-5-24(3)34-43(32)53-55-47-36-26-6-16-17-7(26)28-9-19(17)20-10-29-8(18(16)20)27(6)37-46(36)54(51(41)55)52-42(31)33-23(2)4(14(12)15)25(5)35-44(33)58-56(52)48(37)39(29)50-40(30(9)10)49(38(28)47)57(53)59(45(34)35)60(50)58
InChIKey=AGZHNPDQKMDYHI-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.