An automated transition state search and its application to diverse types of organic reactions

Leif D. Jacobson, Art D. Bochevarov, Mark A. Watson, Thomas F. Hughes, David Rinaldo, Stephan Ehrlich, Thomas B. Steinbrecher, S. Vaitheeswaran, Dean M. Philipp, Mathew D. Halls, and Richard A. Friesner (2017)

Highlighted by Jan Jensen

Copyright 2017 American Chemical Society

Finding transition states remains one of the most labor intensive pursuits in computational chemistry.  While interpolation methods are becoming increasingly robust, they usually require that the atom order for reactant and product are identical (atom mapping) and can be sensitive the starting conformations and relative orientation in case of bi-molecular reactions.  Furthermore, one still has to check whether the right TS is found and formulate a strategy if it is not.  All these things to do not immediately lend themselves to automation but this paper proposes solutions for all these problems.

In particular the paper offers a very elegant solution for the atom mapping problem: bonds are broken in both reactants and products until the connectivity of the fragments are identical after which the atoms in the fragments can be easily matched. Both the comparison and atom mapping of fragments can be easily done with modern cheminformatics toolkits such as RDKit using canonical smiles and  maximum common substructure searchers (after atom order and charge has been removed).  Cases where this fails due to equivalent atoms (e.g. the hydrogens in a methylene group) can then be dealt with by searching for the solution with the lowest RSMD between reactant and product.

The study focussed on relatively small and rigid molecules and issues due to multiple conformations is left for a future publication.

This work is licensed under a Creative Commons Attribution 4.0 International License.

How To Arrive at Accurate Benchmark Values for Transition Metal Compounds: Computation or Experiment?

Y. A. Aoto, A. P. de Lima Batista, A. Köhn, A. G. S. de Oliveira-Filho, J. Chem. Theor. Comput., 2017
Contributed by Theo Keane

Copyright 2017 American Chemical Society 

When performing calculations of any kind, it is important to establish how accurate a method one intends to use is for a given application. Transition metals (TMs) are often problematic systems for computational chemists, because they exhibit “strong correlation”, i.e. either static or dynamic correlation is significant in systems that contain TMs (usually both). This paper adds to the existing literature of benchmark results for TM compounds by performing some rather high-level calculations on 60 diatomic TM compounds. I believe this is intended to improve upon the recent 3dMLBE20 set of Truhlar and co-workers,[1] which was criticised in a pair of papers published in early 2017.[2,3]

In this new benchmarking set, 43 molecules contain first row TMs, 7 contain Ru, Rh or Ag, and the remaining 10 contain Ir, Pt and Au. The multiplicities range from 1 to 7. For these molecules they have assembled experimental data, including bond length, harmonic vibrational frequency and bond dissociation energies. Single reference benchmark values were obtained via (RO/U)CCSD(T)/aug-cc-pwCVnZ-PP[4d, 5d metals]aug-cc-pwCVnZ[else], with n = T, Q, 5, and were extrapolated to the Complete-Basis-Set (CBS) limit. They also investigated the effect of core-valence correlation on the single-reference values. Furthermore, internally contracted Multi-Reference CCSD(T) (icMRCCSD(T)) calculations were performed in the aug-cc-pwCVTZ(-PP) basis, based on full-valence CASSCF reference wavefunctions to investigate the effect of static correlation – the full details of the chosen active spaces are provided in the SI (Table S6). Finally, relativistic effects were considered: scalar relativistic corrections were obtained by comparing frozen core CCSD(T)/aug-cc-pwCVTZ(-PP) calculations with and without the 2nd-order Douglas-Kroll-Hess (DKH2) Hamiltonian. For the 4d and 5d TM containing molecules, Spin-Orbit corrections were obtained from CASSCF calculations with full valence active spaces and the full, 2 electron Breit-Pauli operator. It is important to note that, with the exception of the SO correction, these corrections were not merely calculated for the equilibrium geometry, rather these were calculated at multiple points along the bond length. Overall, the authors have clearly spent a great deal of care ensuring that their ‘benchmark level’ calculations are truly deserving of the title.

An interesting thing to note is that multi-reference, spin-orbit and core-valence correlation corrections all appear to be very weak and sometimes do not improve the agreement with experiment (Table 3). CBS extrapolation is by far the major way to reduce error. This is very important to bear in mind when looking at previous benchmarking results. The authors also note that the usual ‘multireference’ diagnostics are practically useless: there is weak correlation between diagnostics and, more critically, there is very weak correlation between any of the diagnostics and the magnitude of any MR corrections. The M diagnostic[4] is the best performing one; however, it still fails for approximately 30% of cases and yields both false positives and false negatives. The authors also briefly investigate the effect of including 4f orbitals into the correlation treatment for Ir and Pt and find that this has a very weak effect on their results (SI, Table S5).

Finally, the authors use their new benchmark set to rank some functionals. Overall, at the DFT/aug-cc-pVQZ + DKH2 correction level, it appears that hybrid functionals performs on average the best for bond-dissociation energies and equilibrium distances, when compared to the fully corrected results (Table 7). On the other hand, pure functionals perform better for harmonic frequencies. In agreement with the conclusions of the original 3dMLBE20 paper, it is clear that many functionals beat plain CCSD(T)(FC)/aug-cc-pwCVTZ. This reinforces the critical need for CBS extrapolation when performing CC calculations.

(1) Xu, X.; Zhang, W.; Tang, M.; Truhlar, D. G. Do Practical Standard Coupled Cluster Calculations Agree Better than Kohn–Sham Calculations with Currently Available Functionals When Compared to the Best Available Experimental Data for Dissociation Energies of Bonds to 3 D Transition Metals? J. Chem. Theory Comput. 2015, 11 (5), 2036–2052 DOI: 10.1021/acs.jctc.5b00081.
(2) Cheng, L.; Gauss, J.; Ruscic, B.; Armentrout, P. B.; Stanton, J. F. Bond Dissociation Energies for Diatomic Molecules Containing 3d Transition Metals: Benchmark Scalar-Relativistic Coupled-Cluster Calculations for 20 Molecules. J. Chem. Theory Comput. 2017, 13 (3), 1044–1056 DOI: 10.1021/acs.jctc.6b00970.
(3) Fang, Z.; Vasiliu, M.; Peterson, K. A.; Dixon, D. A. Prediction of Bond Dissociation Energies/Heats of Formation for Diatomic Transition Metal Compounds: CCSD(T) Works. J. Chem. Theory Comput. 2017, 13 (3), 1057–1066 DOI: 10.1021/acs.jctc.6b00971.
(4) Tishchenko, O.; Zheng, J.; Truhlar, D. G. Multireference Model Chemistries for Thermochemical Kinetics. J. Chem. Theory Comput. 2008, 4 (8), 1208–1219 DOI: 10.1021/ct800077r.

An Atomistic Fingerprint Algorithm for Learning Ab Initio Molecular Force Fields

Yu-Hang Tang, Dongkun Zhang, and George Em Karniadakis, arXiv:1709.09235
Contributed by Jesper Madsen

Modeling potential energy landscapes of complex atomic environments is challenging. Conventional interatomic potentials are very useful because the potential energy surface is well approximated by some appropriate smooth function of nuclear coordinates. However, choosing the functional form too simple and closed comes with severe limitations because the true potential energy surface may not be (easily) decomposable. 

Instead of sticking with an explicit functional form, one can use continuous density-fields, formed by superimposition of a smoothing kernel on the atoms of the atomic configuration, in order to represent and compare atomistic neighborhoods. Herein, I highlight a recent example of such a method called Density-Encoded Canonically Aligned Fingerprint (DECAF). 

Figure 1: (A) “Two 1D density profiles, ρ1 and ρ2, are generated from two different atomistic configurations using atom-centered smoothing kernel functions. The ‘distance’ between them is measured as the L2 norm of their difference, which corresponds to the highlighted area in the middle plot.” (B) “Shown here is a 2D density field using smoothing kernels whose widths depend on the distances of the atoms from the origin. Darker shades indicate higher density.” 

The preprint by Tang et al. describes the DECAF algorithm (Fig. 1) and also briefly reviews and critically compares with the recent literature of similar methods [such as Smooth Overlap of Atomic Positions (SOAP), Coulomb Matrix, Graph Approximated Energy (GRAPE), and Atom-Centered Symmetry Functions].

The work rests on the key idea of splitting up conventional functional forms into two separate problems, one of representation and one of interpolation, which appears particularly powerful. Molecular fingerprint algorithms such as DECAF are promising in representing atomic neighborhoods faithfully using kernel regression methods. All the beneficial tools and analyses from modern statistics come into play, but there are still open questions that remain. For instance, it is not clear which smoothing kernel, distance metric (and so on) is superior in relating atomic configurations to one-another -- both in general and in specific situations. It is conceivable that there does not exist a best one-size-fits-all option. Furthermore, there will as always be tradeoffs between resolution and computational costs. For an introductory discussion on these topics, the preprint by Tang et al. (and the references within) is a good place to start.

Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model

Bickelhaupt, F. M.; Houk, K. N.,  Angew. Chem. Int. Ed. 2017, 56, 10070-10086
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Bickelhaupt and Houk present a nice review of their separately developed, but conceptually identical model for assessing reactivity.¹ Houk termed this the “distortion/interaction” model,² while Bickelhaupt named it “activation strain”.³ The concept is that the activation barrier can be dissected in a distortion or stain energy associated with bringing the reactants into the geometry of the transition state, and the interaction energy is the stabilization energy afforded by the molecular orbital interactions of the reactant components with each other in the transition state.

The review discusses a broad range of applications, including S_N2 and E₂ reactions, pericyclic reactions (including Diels-Alder reactions of enones and the dehdydro Diels-Alder reaction that I have discussed in this blog), a click reaction, a few examples involving catalysis, and the regioselectivity of indolyne (see this post). They also discuss the role of solvent and the relationship of this model to Marcus Theory.

I also want to mention in passing a somewhat related article by Jorgensen and co-authors published in the same issue of Angewandte Chemie as the above review.⁴ This article discusses the paucity of 10 electron cycloaddition reactions, especially in comparison to the large number of very important cycloaddition reactions involving 6 electrons, such as the Diels-Alder reaction, the Cope rearrangement, and the Claisen rearrangement. While the article does not focus on computational methods, computations have been widely used to discuss 10-electron cycloadditions. The real tie between this paper and the review discussed above is Ken Houk, whose graduate career started with an attempt to perform a [6+4] cycloaddition, and he has revisited the topic multiple times throughout his career.

References

1. Bickelhaupt, F. M.; Houk, K. N., "Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model." Angew. Chem. Int. Ed. 2017, 56, 10070-10086, DOI: 10.1002/anie.201701486.

2. Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity." J. Am. Chem. Soc. 2007, 129, 10646-10647, DOI: 10.1021/ja0734086

3. Bickelhaupt, F. M., "Understanding reactivity with Kohn-Sham molecular orbital theory: E2-S_N2 mechanistic spectrum and other concepts." J. Comput. Chem. 1999, 20, 114-128

4. Palazzo, T. A.; Mose, R.; Jørgensen, K. A., "Cycloaddition Reactions: Why Is It So
Challenging To Move from Six to Ten Electrons?" Angew. Chem. Int. Ed. 2017, 56, 10033-10038, DOI: 10.1002/anie.201701085.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Benzophenone Ultrafast Triplet Population: Revisiting the Kinetic Model by Surface-Hopping Dynamics

Marco Marazzi, Sebastian Mai, Daniel Roca-Sanjuán, Mickaël G. Delcey, Roland Lindh, Leticia González, and Antonio Monari (2016)
Highlighted by Ravi Kumar Venkatraman

In 1967, Norrish and Porter were honoured with Nobel prize for their seminal work on understanding the fast chemical reactions using flash photolysis technique.¹ Since then benzophenone (Bzp) serves as an archetypal system for understanding the photochemistry of various aromatic ketones. Aromatic ketones find their use in various technologically significant applications like sunscreen, photocatalysis, etc., apart from their fundamental interest.² Efficacy of aromatic ketones for use in various applications relies upon their photophysics and photochemistry. Therefore, understanding the photophysics and photochemistry of Bzp has attracted several experimental and theoretical investigations.² Despite these myriads of investigations, pathways for populating the lowest triplet state (T₁) after photoexcitation to the S1 state remains still elusive. There are two plausible pathways: i) a direct ISC from S₁(nπ*) to T₁(nπ*); or ii) an indirect process, involving ISC from S₁(nπ*) to T₁(ππ*) with subsequent internal conversion (IC) to T₁(nπ*). The latter pathway is more efficient, according to El-Sayed’s rule, because it entails a change in the orbital character during the spin-orbit coupling mediated process.³

Reproduced with permission from Marco Marazzi, Sebastian Mai, et. al., J. Phys. Chem. Lett., 7, 622 (2016) under Creative Commons Attribution (CC-BY) License

In this work, authors have employed ab initio surface-hopping dynamics simulation for Bzp in gas phase to explore the pathways for the lowest triplet state (T₁) population after photo-excitation to the S₁ state. This study clearly demonstrates that the dominant mechanism for populating the T₁ state is the indirect pathway invoking T₂ state as an intermediate. This study urges reinvestigation of spectroscopic assignment for Bzp in various time-resolved spectroscopic techniques. Furthermore, the mechanism for the photoinduced energy transfer in photocatalysis and DNA damage studies must be revisited as in principle now both channels involving T₂ and T₁ states are available.

References:
1.) F. Ariese, K. Roy, V. R. Kumar, H. C. Sudeeksha, S. Kayal, S. Umapathy, Time-Resolved Spectroscopy: Instrumentation and Applications in Encyclopedia of Analytical Chemistry, edited by R. A. Meyers, 1-55, (2017) John Wiley & Sons, Ltd.
2.) M. C. Cuquerella, V. L-Vallet, J. Cadet, and M. A. Miranda, Benzophenone Photosensitized DNA Damage, Acc. Chem. Res., 45, 1558 (2012).
3.) Elsayed, M. A., Spin-Orbit Coupling and Radiationless Processes in Nitrogen Heterocyclics. J. Chem. Phys., 38, 2834 (1963).

More applications of computed NMR spectra

Grimblat, N.; Kaufman, T. S.; Sarotti, A. M., "Computational Chemistry Driven Solution to Rubriflordilactone B." Org. Letters 2016, 18, 6420-6423
Reddy, D. S.; Kutateladze, A. G., "Structure Revision of an Acorane Sesquiterpene Cordycepol A." Org. Letters 2016, 18, 4860-4863
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

In this post I cover two papers discussing application of computed NMR chemical shifts to structure identification and (yet) another review of computational techniques towards NMR structure prediction.

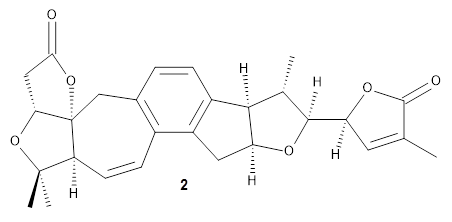
Grimblat, Kaufman, and Sarotti¹ take up the structure of rubriflordilactone B 1, which was isolated from Schisandra rubriflora. The compound was then synthesized and its x-ray structure reported, however its NMR did not match with the natural extract. It was suggested that there were actually two compounds in the extract, the minor one was less soluble and is the crystallized 1, and a second compound responsible for the NMR signal.

The authors looked at all stereoisomers of this molecule keeping the three left-most rings intact. The low energy rotamers of these 32 stereoisomers were then optimized at B3LYP/6-31G* and the chemical shifts computed at PCM(pyridine)/mPW1PW91/6-31+G**. To benchmark the method, DP4+ was used to identify which stereoisomer best matches with the observed NMR of authentic 1; the top fit (92.6% probability) was the correct structure.

The 32 stereoisomers were then tested against the experimental NMR of the natural extract. DP4+ with just the proton shifts suggested structure 2 (99.8% probability); however, the ¹³C chemical shifts predicted a different structure. Re-examination of the reported chemical shifts identifies some mis-assigned signals, which led to a higher C-DP4+ prediction. When all 128 stereoisomers were tested, structure 2 had the highest DP4+ prediction (99.5%), but the C-DP4+ prediction remained problematic (10.8%). Analyzing the geometries of all reasonable alternative for agreement with the NOESY spectrum confirmed 2. These results underscore the importance of using all data sources.

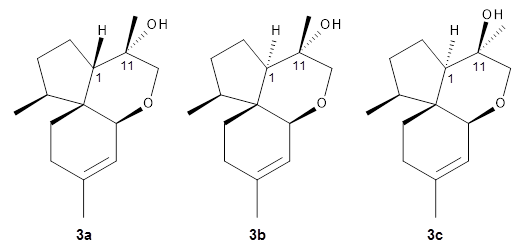
Reddy and Kutateladze point out the importance of using coupling constants along with chemical shifts in structure identification.² They examined cordycepol A 3, obtained from Cordyceps ophioglossoides. They noted that the computed chemical shifts and coupling constants of originally proposed structure 3adiffered dramatically from the experimental values.

They first proposed that the compound has structure 3b. The computed coupling constants using their relativistic force field.³ The experimental coupling constants for the proton H1 are 13.4 and 7.1 Hz. The computed values for 3a are 8.9 and 1.6 Hz, and this structure is clearly incorrect. The coupling constants are improved with 3b, but the ¹³C chemical shifts are in poor agreement with experiment. So, they proposed structure 3c, the epimer at both C1 and C11 of the original structure.

They optimized four conformations of 3c at B3LYP/6-31G(d) and obtained Boltzmann-weighted chemical shifts at mPW1PW91/6-311+G(d,p). The RMS deviation of the computed ¹³C chemical shifts relative to the experiment is only 1.54 ppm, and more importantly, the computed coupling constants of 13.54 and 6.90 Hz are in excellent agreement with the experiment values.

Lastly, Grimblat and Sarotti present a review of a number of methods for using computed NMR chemical shifts towards structure prediction.⁴ These methods include CP3, DP4, DP4+ (all of which I have posted on in the past) and an artificial neural network approach of their own design. They discuss a number of interesting cases where each of these methods has been crucial in identifying the correct chemical structure.

References

1. Grimblat, N.; Kaufman, T. S.; Sarotti, A. M., "Computational Chemistry Driven Solution to Rubriflordilactone B." Org. Letters 2016, 18, 6420-6423, DOI: 10.1021/acs.orglett.6b03318.

2. Reddy, D. S.; Kutateladze, A. G., "Structure Revision of an Acorane Sesquiterpene Cordycepol A." Org. Letters 2016, 18, 4860-4863, DOI: 10.1021/acs.orglett.6b02341.

3. (a) Kutateladze, A. G.; Mukhina, O. A., "Minimalist Relativistic Force Field: Prediction of Proton–Proton Coupling Constants in 1H NMR Spectra Is Perfected with NBO Hybridization Parameters." J. Org. Chem.2015, 80, 5218-5225, DOI: 10.1021/acs.joc.5b00619; (b) Kutateladze, A. G.; Mukhina, O. A., "Relativistic Force Field: Parametrization of 13C–1H Nuclear Spin–Spin Coupling Constants." J. Org. Chem. 2015, 80, 10838-10848, DOI: 10.1021/acs.joc.5b02001.

4. Grimblat, N.; Sarotti, A. M., "Computational Chemistry to the Rescue: Modern Toolboxes for the Assignment of Complex Molecules by GIAO NMR Calculations." Chem. Eur. J. 2016, 22, 12246-12261, DOI: h10.1002/chem.201601150.

InChIs

1: InChI=1S/C28H30O6/c1-13-9-20(32-26(13)30)25-14(2)24-17-6-5-15-12-28-21(8-7-16(15)18(17)10-19(24)31-25)27(3,4)33-22(28)11-23(29)34-28/h5-9,14,19-22,24-25H,10-12H2,1-4H3/t14-,19+,20-,21-,22+,24-,25-,28+/m0/s1
InChIKey=JGSLSHOXBXVVTQ-NEUKEVNNSA-N

2: InChI=1S/C28H30O6/c1-13-9-20(32-26(13)30)25-14(2)24-17-6-5-15-12-28-21(8-7-16(15)18(17)10-19(24)31-25)27(3,4)33-22(28)11-23(29)34-28/h5-9,14,19-22,24-25H,10-12H2,1-4H3/t14-,19-,20-,21-,22+,24+,25-,28+/m0/s1
InChIKey=JGSLSHOXBXVVTQ-WQIRXNRDSA-N

3c: InChI=1S/C16H28O2/c1-6-11(2)9-14-16(5)12(3)7-8-13(16)15(4,17)10-18-14/h9,12-14,17H,6-8,10H2,1-5H3/b11-9-/t12-,13-,14-,15-,16+/m0/s1
InChIKey=WPQIVUHVYBQTBG-AWEVENECSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.