Comparison of Molecular Mechanics, Semi-Empirical Quantum Mechanical, and Density Functional Theory Methods for Scoring Protein−Ligand Interactions

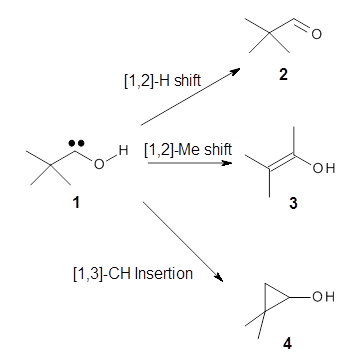
Nusret D. Yilmazer and Martin Korth Journal of Physical Chemistry B 2013, 117, 8075
Contributed by +Jan Jensen

This paper provides an extremely thorough comparison of electronic protein-ligand interaction energies computed using MM force fields, semi-empirical methods, and DFT.

About 700 protein-ligand complexes were selected from the PDBbind2007 database and four model systems of increasing size (including atoms up to 10 Å from a ligand atom) are created for each. DFT calculations were only possible for around 500 complexes using a 5 Å cutoff, and MM calculations were only possible for 352 complexes due to parameterization problems. 

Single point energies for the protein-ligand complex and separated protein and ligand are then computed and used to compute interaction energies, which were then compared amongst each other.  For example, systems of different size and be compared to monitor convergence and different methods can be compared for a given cutoff.  

Some of the more interesting comparisons to me are PM6-DH+ vs BP86-D2/TZVP (R = 1.00) and MMFF94 vs BP86-D2/TZVP (R = 0.93).  (Interestingly, the former value decreases to 0.92 if COSMO is included - that is unexpected to me.)  While these R values are quite good the corresponding MAD values are quite bad: 14 and 57 kcal/mol, respectively!  I find the former quite surprising since the error in the PM6-DH+ hydrogen bond strengths computed for the underlying training set are on the order of 2 kcal/mol. It could be non-additivity or more interactions between charged groups in the present set.

Acknowledgement: thanks to +Jimmy Charnley Kromann for alerting me to this paper

This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Predicting Kinetically Unstable C-C Bonds from the Ground-State Properties of a Molecule

Markopoulos, G.; Grunenberg, J. Angew. Chem. Int. Ed. 2013, 52, 10648
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Can one identify a labile bond in a molecule without computing activation barriers? Markopoulos and Grunenberg suggest that examination of the bond length and its associated relaxed force constant might provide some guidance.¹

The relaxed force constant comes from identifying the force constant for some coordinate while allowing for other coordinates to relax. Badger’s rule relates the (normal) force constant to bond distance (k = a/(r_eq – d)³). For a series of 36 molecules, covering 71 C-C single bonds, Badger’s rule fits the data well, except for a set of molecules which undergo rapid Cope rearrangements (like bullvalene and semibullvalene). For these molecules, the relaxed force constants are much lower than Badger’s rule predicts, and indicates a weakened bond. This gives rise to their low activation barriers.

Another example is provided with the highly strained polycyclic hydrocarbon 1. This compound is predicted (B3LYP/6-31G(d)) to undergo a [1,2]-shift to give the carbene 2 (see Figure 1), and this is extremely exothermic: -105.7 kcal mol^-1, reflecting the enormous strain of 1. The barrier, through TS1 (Figure 1), is only 6.7 kcal mol^-1. This rearrangement was predicted by examining the relaxed force constants which identified a very weak bond, despite a short bond distance of 1.404 Å. It is unlikely that without this guidance, one would have predicted that this short bond is likely to rupture and produce this particular product.

1	2
TS1

Figure 1. B3LYP/6-31G(d) optimized structures of 1, 2, and TS1.

References

(1) Markopoulos, G.; Grunenberg, J. "Predicting Kinetically Unstable C-C Bonds from the Ground-State Properties of a Molecule," Angew. Chem. Int. Ed. 2013, 52, 10648-10651, DOI: 10.1002/anie.20130382.

InChIs

1: InChI=1S/C14H12/c1-2-8-11-5-3-9-7(1)10(9)4-6-12(8,11)14(8,11)13(7,9)10/h1-6H2
InChIKey=LNBZAENQMFDBJW-UHFFFAOYSA-N

2: InChI=1S/C14H12/c1-3-11-12-4-2-9-7-8(1,9)10(9)5-6-13(11,12)14(10,11)12/h1-6H2
InChIKey=UKVODHRLGFPZPT-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Tunneling control of chemical reactions: C-H insertion versus H-tunneling in tert-butylhydroxycarbene

Ley, D.; Gerbig, D.; Schreiner, P. R. Chem. Sci. 2013, 4, 677
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Sorry I missed this paper from much earlier this year – it’s from a journal that’s not on my normal reading list. Anyways, here is another fantastic work from the Schreiner lab demonstrating the concept of tunneling control (see this post).¹ They prepare the t-butylhydroxycarbene 1 at low temperature to look for evidence of formation of possible products arising from a [1,2]-hydrogen shift (2), a [1,2]-methyl shift (3) or a [1,3]-CH insertion (4).

Schreiner performed CCSD(T)/cc-pVDZ optimizations of these compounds along with the transition states for the three migrations. The optimized geometries and relative energies are shown in Figure 1. The thermodynamic product is the aldehyde 2 while the kinetic product is the cyclopropane 4, with a barrier of 23.8 kcal mol^-1 some 3.5 kcal mol^-1 lower than the barrier leading to 2.

1 (0.0)	TS2 (27.3)	2 (-53.5)
	TS3 (31.0)	3 (-41.0)
	TS4 (23.8)	4 (-28.3)

Figure 1. CCSD(T)/cc-pVDZ optimized structures of 1-4 and the transition states for the three reaction. Relative energies in kcal mol^-1.

At low temperature (11 K), 1 is found to slowly convert into 2 with a half-life of 1.7 h. No other product is observed. Rates for the three reactions were also computed using the Wentzel-Kramers-Brillouin (WKB) method (which Schreiner and Allen have used in all of their previous studies). The predicted rate for the conversion of 1 into 2, which takes place at 11 K solely through a tunneling process, is 0.4h, in quite reasonable agreement with experiment. The predicted rates for the other two potential reactions at 11 K are 10³¹ and 10⁴⁰ years.

This is clearly an example of tunneling control. The reaction occurs not across the lowest barrier, butthrough the narrowest barrier.

References

(1) Ley, D.; Gerbig, D.; Schreiner, P. R. "Tunneling control of chemical reactions: C-H insertion versus H-tunneling in tert-butylhydroxycarbene," Chem. Sci. 2013, 4, 677-684, DOI: 10.1039/C2SC21555A.

InChI

1: InChI=1S/C5H10O/c1-5(2,3)4-6/h6H,1-3H3
InChIKey=ZGFKBRGJTPEEOC-UHFFFAOYSA-N

2: InChI=1S/C5H10O/c1-5(2,3)4-6/h4H,1-3H3

3: InChI=1S/C5H10O/c1-4(2)5(3)6/h6H,1-3H3
InChIKey=BZAZNULYLRVMSW-UHFFFAOYSA-N

4: InChI=1S/C5H10O/c1-5(2)3-4(5)6/h4,6H,3H2,1-2H3
InChIKey=MWWQKEGWQLBJBJ-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.