ChemDyME: Kinetically Steered, Automated Mechanism Generation Through Combined Molecular Dynamics and Master Equation Calculations

Robin J. Shannon, Emilio Martínez-Núñez, Dmitrii V. Shalashilin, David R. Glowacki (2021)
Highlighted by Jan Jensen

Figure 1 from the paper (c) The authors 2021. Reproduced under the CC-BY license

ChemDyME couples metadynamics statistical  rate  theory to automatically find kinetically important reactions and then solve the time evolution of the species in the evolving network. 

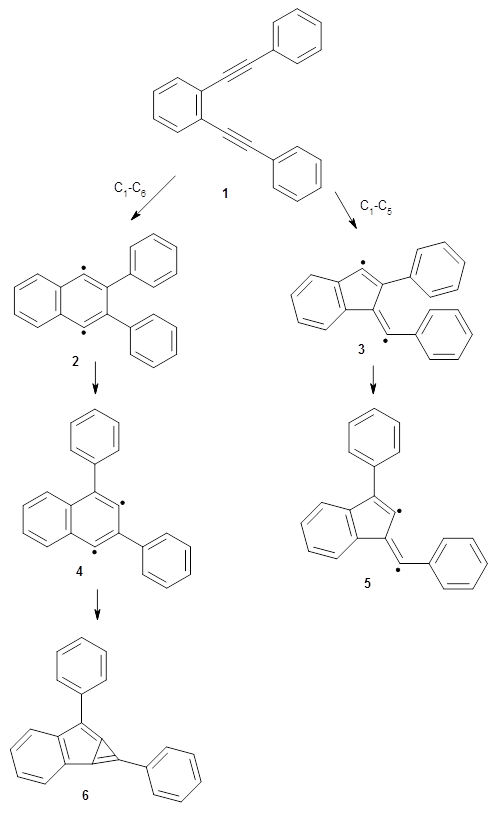
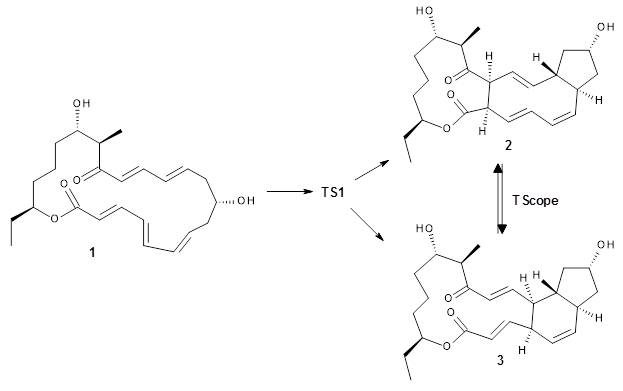
There are three steps as shown in the figure above:

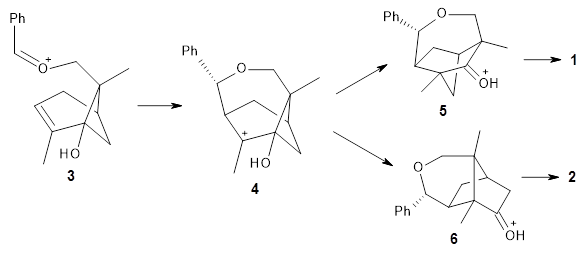
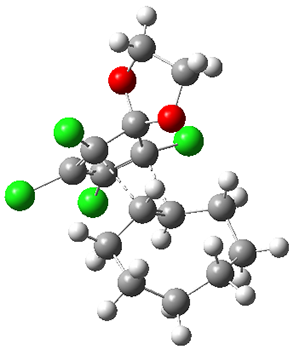
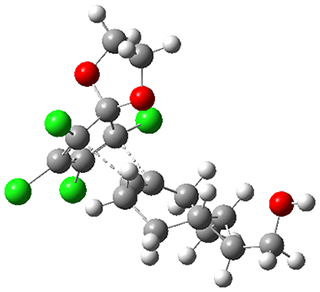
1. Molecular Dynamics (MD) where semiempirical metadynamics simulations are used to identify products that are likely to be connected to the reactant by low barriers. Specifically the boxed MD (BXD) metadynamics method where an extra term to the atomic velocities to steer the MD away from previously explored regions of configuration space. The MD stops when changes in atomic connectivity is detected.

2. Optimisation and Refinement (OR) where the products structures are optimised an the TSs to the reactant are located at a higher level of theory. The initial guess for the TS geometry is the first structure in the trajectory where the atomic connectivity changes. If that approach fails a spline-based reaction path method is used. The TSs are verified by IRCs.

3. Master Equation (ME) where the set of coupled kinetic equations are solved numerically. As the reaction network grows this can become computationally demanding, which is a problem when it is done on-the-fly. The authors therefore employ the Boxed Molecular Kinetics approach to speed things up.

These steps are then repeated using the kinetically most accessible product (identified by the ME step) as the reactant. The entire procedure is then repeated until a desired maximum reaction time is reached.

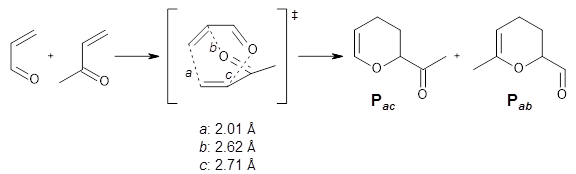
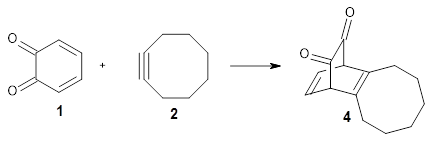
The authors test the procedure on two well studies systems and show that the procedure indeed identifies the most important reactions in the reaction network.

Disclaimer: My group has developed a similar approach for the first two steps.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Deflate to Understand Complex Molecular Kinetics

Brooke E. Husic & Frank Noé. arXiv: 1907.04101

Contributed by Jesper Madsen

Dimensionality reduction is at the core of understanding and making intuitive sense of complex dynamic phenomena in chemistry.  It is usually assumed that the slowest mode is the one of primary interest; however, it is critical to realize that this is not always so! A conceptual example hereof is a protein folding simulation (Lindorff-Larsen et al. Science 334, 517-520, 2011) where the slowest dynamical mode is not the folding itself (see Figure). What is the influence, then, of “non-slowest” modes in this process and how can it most appropriately be elucidated?

FIG: Figure 2 from the preprint: "(A) Sampled villin structures from the MD trajectory analyzed. Helical secondary structure is colored and coils are white. Each image represents five structures sampled from similar locations in TIC space as determined by a 250-center k-means model built upon the first three original TICs. The purple structure represents the folded state, and the blue structure represents the denatured state. The green structure is a rare helical misfolded state that we assert is an artifact. (B) Two-dimensional histograms for TICA transformations constructed from villin contact distances. Dashed lines indicate the regions corresponding to the sampled structures of the same color. The first TIC tracks the conversion to and from the rare artifact only. The second TIC tracks the majority of the folding process and correlates well with RMSD to the folded structure."

This work by Husic and Noé show how deflation can provide an answer to these questions. Technically speaking deflation is a collection of methods for how to modify a matrix after the largest eigenvalue is known in order to find the rest. In their provided example of the folding simulation, the dominant Time-lagged Independent Component (TIC) encapsulates the "artifact" variation that we are not really interested in. Thus, a constructed kinetic (Markov-state) model will be contaminated in several undesirable ways as discussed by the authors in great detail.  

In principle, this should be a very common problem since chemical systems have complex Hamiltonians. Perhaps the reason why we don’t see it discussed more is that ultra-rare events – real or artifact – may not usually be sampled during conventional simulations. So, with the increasing computational power available to us, and simulations approaching ever-longer timescales, this is likely something that we need to be able to handle. This preprint describes well how one can think about attacking these potential difficulties.   

Artificial Intelligence Assists Discovery of Reaction Coordinates and Mechanisms from Molecular Dynamics Simulations

Hendrik Jung, Roberto Covino, and Gerhard Hummer. arXiv: 1901.04595

Contributed by Jesper Madsen

Here, I highlight a recent preprint describing an application of Artificial Intelligence/Machine Learning (AI/ML) methods to problems in computational chemistry and physics. The group previously published the intrinsic map dynamics (iMapD) method, which I also highlighted here on Computational Chemistry Highlights. The basic idea in the previous study was to use an automated trajectory-based approach (as opposed to a collective variable-based approach) to explore the free-energy surface a computationally expensive Hamiltonian that describes a complex biochemical system.

Fig 1: Schematic flow chart of the AI-assisted MD simulation algorithm.

The innovation in their current approach is the combination of the sampling scheme, statistical inference, and deep learning to construct a framework where sampling and mechanistic interpretation happens simultaneously – an important milestone towards completely “autonomous production and interpretation of MD simulations of rare events,” as the authors themselves remark.

It is reassuring to see that the method correctly identifies known results for benchmark cases (the alanine dipeptide and LiCl dissociation) and out-competes traditional approaches such as transition path sampling in terms of efficiency. In these simple model cases, however, complexity is relatively low and sampling is cheap. I will be looking forward to seeing the method applied to a much more complex problem in the future; E.g. a problem where ergodicity is a major issue other challenges, such as hysteresis, plays a significant role.

Another much appreciated aspect of general interest in this paper that I am emphasizing is the practical approach to interpretation of the constructed neural networks. All in all, there are many useful comments and observations in this preprint and I would recommend reading it thoroughly for those who seek to use modern AI-based methods on molecular simulations.

Rearrangement of Hydroxylated Pinene Derivatives to Fenchone-Type Frameworks: Computational Evidence for Dynamically-Controlled Selectivity

Blümel, M.; Nagasawa, S.; Blackford, K.; Hare, S. R.; Tantillo, D. J.; Sarpong, R., J. Am. Chem. Soc. 2018, 140, 9291-9298
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Sarpong and Tantillo have examined the acid-catalyzed Prins/semipinacol rearrangement of hydroxylated pinenes, such as Reaction 1.¹

Rxn 1

Interestingly, only the fenchone scaffold products, like 1, are observed and the camphor scaffold products, like 2, are not observed. Cation intermediates are likely, and this means that a primary alkyl shift is taking place in preference to a tertiary alkyl shift, see Scheme 1.

Scheme 1.

Primary alkyl shift

Tertiary alkyl shift

They proposed the following key steps in the reaction mechanism:

ωB97X-D/6-31+G(d,p) computations find a flat surface around cation intermediate 4: the TS leading to 5and 6 are only 1.3 and 3.3 kcal mol^-1, respectively. Since these small barriers are quite susceptible to changes in basis set and functional, and since Tantillo has found many examples of post-transition state bifurcations in cation systems, the authors reasonably decided to conduct molecular dynamics trajectories originating at the TS connecting 3 and 4. The geometries of the critical points are shown in Figure 1.

The trajectory study shows all the usual characteristics of reactions that are under dynamic control. A third of the trajectories show recrossing of the barrier, typical of very flat surfaces. Nearly all of the remaining trajectories led to 5, with only 2 trajectories (~1%) leading to 6. The dynamics are understandable in terms of favoring the primary alkyl shift over the tertiary since a significantly smaller mass needs to move in the former case.

TS 3 → 4
4
TS 4 → 5	TS 4 → 6

Figure 1. ωB97X-D/6-31+G(d,p) optimized geometries.

This is yet another study that implicates dynamic effects in routine reactions, one of many I have discussed over the years.

References

1. Blümel, M.; Nagasawa, S.; Blackford, K.; Hare, S. R.; Tantillo, D. J.; Sarpong, R., "Rearrangement of Hydroxylated Pinene Derivatives to Fenchone-Type Frameworks: Computational Evidence for Dynamically-Controlled Selectivity." J. Am. Chem. Soc. 2018, 140, 9291-9298, DOI: 10.1021/jacs.8b05804.

InChIs

1: InChI=1S/C17H20O2/c1-16-9-12-8-13(16)14(11-6-4-3-5-7-11)19-10-17(12,2)15(16)18/h3-7,12-14H,8-10H2,1-2H3/t12?,13?,14-,16?,17?/m0/s1
InChIKey=LTTUIPPXEHHMJS-XWTIBIIYSA-N

2: InChI=1S/C17H20O2/c1-16-10-19-15(11-6-4-3-5-7-11)13-8-12(16)9-14(18)17(13,16)2/h3-7,12-13,15H,8-10H2,1-2H3/t12?,13?,15-,16?,17?/m0/s1
InChIKey=GCKIOHNLJYVWKL-CMESGNGWSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Readily Accessible Ambiphilic Cyclopentadienes for Bioorthogonal Labeling

Levandowski, B. J.; Gamache, R. F.; Murphy, J. M.; Houk, K. N., J. Am. Chem. Soc. 2018, 140, 6426-6431
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

I recently posted on a paper proposing 1,2-benzoquinone and related compounds as the diene component for bioorthogonal labeling. Levandowski, Gamache, Murphy, and Houk report on tetrachlorocyclopentadiene ketal 1 as an active ambiphilic diene component.¹

1 is sterically congested to diminish self-dimerization and will react with both electron-rich and electron-poor dienes. To test it as an active diene in bioorthogonal labeling applications, they optimized the structures of the transition states at CPCM(water)/M06-2X/6-311+G(d,p)//CPCM(water)/M06-2X/6-31G(d) for the Diels-Alder reaction of 1 with a variety of dienophiles including trans-cyclooctene 2 and endo-bicyclononyne 3. These transition states are shown in Figure 1. The activation free energy is quite low for each: 18.1 kcal mol^-1 with 2 and 18.9 kcal mol^-1 with 3.

TS(1+2)

TS(1+3)

Figure 1. CPCM(water)/M06-2X/6-31G(d) optimized geometries for the TSs of the reaction of 1 with 2and 3.

Experiments were successfully run using 1 as a label on a neuropeptide.

References

1) Levandowski, B. J.; Gamache, R. F.; Murphy, J. M.; Houk, K. N., "Readily Accessible Ambiphilic Cyclopentadienes for Bioorthogonal Labeling." J. Am. Chem. Soc. 2018, 140, 6426-6431, DOI: 10.1021/jacs.8b02978.

InChIs

1:InChI=1S/C7H4Cl4O2/c8-3-4(9)6(11)7(5(3)10)12-1-2-13-7/h1-2H2
InChIkey=DXQQKKGWMVTLOJ-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

MD studies of simple pericyclic reactions

Mackey, J. L.; Yang, Z.; Houk, K. N., "Dynamically concerted and stepwise trajectories of the Cope rearrangement of 1,5-hexadiene." Chem. Phys. Lett. 2017, 683, 253-257
Yang, Z.; Zou, L.; Yu, Y.; Liu, F.; Dong, X.; Houk, K. N., "Molecular dynamics of the two-stage mechanism of cyclopentadiene dimerization: concerted or stepwise?" Chem. Phys. 2018, in press
Yang, Z.; Dong, X.; Yu, Y.; Yu, P.; Li, Y.; Jamieson, C.; Houk, K. N., "Relationships between Product Ratios in Ambimodal Pericyclic Reactions and Bond Lengths in Transition Structures." J. Am. Chem. Soc. 2018, 140, 3061-3067
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

At the recent ACS meeting in New Orleans, Ken Houk spoke at the Dreyfus award session in honor of Michele Parrinello. Ken’s talk included discussion of some recent molecular dynamics studies of pericyclic reactions. Because of their similarities in approaches and observations, I will discuss three recent papers from his group (which Ken discussed in New Orleans) in this post.

The Cope rearrangement, a fundamental organic reaction, has been studied extensively by computational means (see Chapter 4.2 of my book). Mackey, Yang, and Houk examine the degenerate Cope rearrangement of 1,5-hexadiene with molecular dynamics at the (U)B3LYP/6-31G(d) level.¹ They examined 230 trajectories, and find that of the 95% of them that are reactive, 94% are trajectories that directly cross through the transition zone. By this, Houk means that the time gap between the breaking and forming C-C bonds is less than 60 fs, the time for one C-C bond vibration. The average time in the transition zone is 35 fs. This can be thought of as “dynamically concerted”. For the other few trajectories, a transient diradical with lifetime of about 100 fs is found.

The dimerization of cyclopentadiene finds the two [4+2] pathways merging into a single bispericylic transition state. ² Only a small minority (13%) of the trajectories sample the region about the Cope rearrangement that interconverts the two mirror image dimers. These trajectories average about 60 fs in this space, which comes from the time separation between the formation of the two new C-C bonds. The majority of the trajectories quickly pass through the dimerization transition zone in about 18 fs, and avoid the Cope TS region entirely. These paths can be thought of as “dynamically concerted”, while the other set of trajectories are “dynamically stepwise”. It should be noted however that the value of S² in the Cope transition zone are zero and so no radicals are being formed.

Finally, Yang, Dong, Yu, Yu, Li, Jamieson, and Houk examined 15 different reactions that involve ambimodal (i.e. bispericyclic) transition states.³ They find a strong correlation between the differences in the bond lengths of the two possible new bond vs. their product distribution. So for example, in the reaction shown in Scheme 1, bond a is the one farthest along to forming. Bond b is slightly shorter than bond c. Which of these two is formed next is dependent on the dynamics, and it turns out the P_ab is formed from 73% of the trajectories while P_ac is formed only 23% of the time. This trend is seen across the 15 reaction, namely the shorter of bond b or c in the transition state leads to the larger product formation. When competing reactions involve bonds with differing elements, then a correlation can be found with bond order instead of with bond length.

Scheme 1

References

1) Mackey, J. L.; Yang, Z.; Houk, K. N., "Dynamically concerted and stepwise trajectories of the Cope rearrangement of 1,5-hexadiene." Chem. Phys. Lett. 2017, 683, 253-257, DOI: 10.1016/j.cplett.2017.03.011.

2) Yang, Z.; Zou, L.; Yu, Y.; Liu, F.; Dong, X.; Houk, K. N., "Molecular dynamics of the two-stage mechanism of cyclopentadiene dimerization: concerted or stepwise?" Chem. Phys. 2018, in press, DOI: 10.1016/j.chemphys.2018.02.020.

3) Yang, Z.; Dong, X.; Yu, Y.; Yu, P.; Li, Y.; Jamieson, C.; Houk, K. N., "Relationships between Product Ratios in Ambimodal Pericyclic Reactions and Bond Lengths in Transition Structures." J. Am. Chem. Soc. 2018,140, 3061-3067, DOI: 10.1021/jacs.7b13562.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Automated Transition State Theory Calculations for High-Throughput Kinetics

Pierre L. Bhoorasingh, Belinda L. Slakman, Fariba Seyedzadeh Khanshan, Jason Y. Cain, and Richard H. West (2017)
Highlighted by Jan Jensen

Figure 1 from Bhoorasingh et al. J. Phys. Chem. A 2017, 121, 6896. 

Copyright 2017 American Chemical Society

I have written about automated transition state searching before, so I was interested to see how this work differed. Both methods aim at obtaining the best possible guess of the TS structure, which is then used as a starting point for a conventionional TS optimization. In the current work this is done by estimating bond lengths between the reacting atoms using a group contribution method based on known TS structures. These distances are then constrained while a conformational search is performed for the rest of the molecular structure using the UFF force field. The method is described in more detail here.

This approach is thus not too different from the TS template structure approach used in the Schrödinger study, but goes on to perform a conformational search for the TS, which the Schrödinger study did not. So it indeed encouraging to see that the conformational search seems to work and give reasonable results.

Both approaches requires that the atom orders are the same in the reactants and products. In general this is a hard problem and the Schrödinger paper offers one approach to this. However, in the current study the products are automatically generated from the reactants using the Reaction Mechanism Generator (RMG) program in such a way (I believe) that the atom order is preserved.

So if you're interested in a particular TS the current approach is unlikely to be useful since it is rather intimately tied to the RMG program and certain types of chemical reactions. However, if you are interested in these types of chemical reactions then the approach seems quite useful since the entire process is automated and appears quite robust. 

More importantly is an important proof-of-concept of what is possible in terms of automation given a large an carefully constructed training set of chemical reactions.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Kinetics of the Strain-Promoted Oxidation-Controlled Cycloalkyne-1,2-quinone Cycloaddition: Experimental and Theoretical Studies

Escorihuela, J.; Das, A.; Looijen, W. J. E.; van Delft, F. L.; Aquino, A. J. A.; Lischka, H.; Zuilhof, H., J. Org. Chem. 2018, 83, 244
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Click chemistry has been used in a broad range of applications. The use of metal catalysts has limited its application to biological system, but the development of strain-promoted cycloaddition to cyclooctyne has opened up click chemistry to bioorthogonal labelling.

An interesting variation on this is the use of 1,2-benzoquinone 1 and substituted analogues as the Diels-Alder diene component. Escorihuela and co-workers have reported on the use of this diene with a number of cyclooctyne derivatives, measuring kinetics and also using computations to assess the mechanism.¹

Their computations focused on two reactions using cyclooctyne 2 and the cyclopropane-fused analogue 3:

	Reaction 1
	Reaction 2

They examined these reactions with a variety of density functionals along with some post-HF methods. The transition states of the two reactions are shown in Figure 1. A variety of different density functionals and MP2 are consistent in finding synchronous or nearly synchronous transition states.

Rxn1-TS

Rxn2-TS

Figure 1. B97D/6-311+G(d,p) transition states for Reactions 1 and 2.

In terms of activation energies, all of the DFT methods consistently overestimate the barrier by about 5-10 kcal mol^-1, with B97D-D3 doing the best. MP2 drastically underestimates the barriers, though the SOS-MP2 or SCS-MP2 improve the estimate. Both CCSD(T) and MR-AQCC provide estimates of about 8.5 kcal mol^-1, still 3-4 kcal mol^-1 too high. The agreement between CCSD(T), a single reference method, and MR-AQCC, a multireference method, indicate that the transition states have little multireference character. Given the reasonable estimate of the barrier afforded by B97D-D3, and its tremendous performance advantage over SCS-MP2, CCSD(T) and MR-AQCC, this is the preferred method (at least with current technology) for examining Diels-Alder reactions like these, especially with larger molecules.

References

1) Escorihuela, J.; Das, A.; Looijen, W. J. E.; van Delft, F. L.; Aquino, A. J. A.; Lischka, H.; Zuilhof, H., "Kinetics of the Strain-Promoted Oxidation-Controlled Cycloalkyne-1,2-quinone Cycloaddition: Experimental and Theoretical Studies." J. Org. Chem. 2018, 83, 244-252, DOI: 10.1021/acs.joc.7b02614.

InChIs

1: InChI=1S/C6H4O2/c7-5-3-1-2-4-6(5)8/h1-4H
InChIKey=WOAHJDHKFWSLKE-UHFFFAOYSA-N

2: InChI=1S/C8H12/c1-2-4-6-8-7-5-3-1/h1-6H2
InChIKey=ZPWOOKQUDFIEIX-UHFFFAOYSA-N

3: InChI=1S/C9H12/c1-2-4-6-9-7-8(9)5-3-1/h8-9H,3-7H2
InChIKey=rQDNSAFCVPAMWCJ-UHFFFAOYSA-N

4: InChI=1S/C14H16O2/c15-13-11-7-8-12(14(13)16)10-6-4-2-1-3-5-9(10)11/h7-8,11-12H,1-6H2
InChIKey=OQMYZEFKUMPECV-UHFFFAOYSA-N

5: InChI=1S/C15H16O2/c16-14-12-5-6-13(15(14)17)11-4-2-9-7-8(9)1-3-10(11)12/h5-6,8-9,12-13H,1-4,7H2/t8-,9+,12?,13?
InChIKey=NKDGTIVNLDJQKR-RFZWMSCOSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Enediyne Cyclization on Au(111)

de Oteyza, D. G.; Paz, A. P.; Chen, Y.-C.; Pedramrazi, Z.; Riss, A.; Wickenburg, S.; Tsai, H.-Z.; Fischer, F. R.; Crommei, M. F.; Rubio, A. J. Amer. Chem. Soc. 2016, 138, 10963–10967
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

The Bergman cyclization and some competitive reactions are discussed in detail in Chapter 4 of by book. The Bergman cyclization makes the C₁-C₆ bond from an enediyne. Another, but rarer, option is to make the C₁-C₅ bond, the Schreiner-Pascal cyclization pathway. de Oteyza and coworkers have examined the competition between these two pathways for 1 on a gold surface, and used STM and computations to identify the reaction pathway.¹

The two pathways are shown below. The STM images identify 1 as the reactant on the gold surface and the product is 6. No other product is observed.

Projector augmented wave (PAW) pseudo-potential computations using the PBE functional were performed for the reaction on a Au (111) surface was modeled by a 7 x 7 x 3 supercell. The optimized geometries of the critical points are show in Figure 1.

1
TS(1→2)	TS(1→3)
2	3
TS(2→6)	TS(3→5)
6	5

Figure 1. Optimized geometries of the critical points on the two reaction pathways.

Explicit values of the relative energies are not given in either the paper or the supporting information, but rather a plot shows the relative positions of the critical points. The important points are the following: (a) the barrier for the C₁-C₅ cyclization is lower than the barrier for the C₁-C₆ cyclization and 3 is lower in energy than 2; (b) 5 is lower in energy than 6; and (c) the barrier for taking 2 to 6 is significantly below the barrier taking 3 into 5. The barrier for the phenyl migration taking 3 into 5 is so high because of a strong interaction between the carbon radical and a gold atom of the surface. The authors suggest that the two initial cyclizations are reversible, but the very high barrier for forming 5 precludes it from taking place, leaving only the route to 6 as a viable pathway.

References

(1) de Oteyza, D. G.; Paz, A. P.; Chen, Y.-C.; Pedramrazi, Z.; Riss, A.; Wickenburg, S.; Tsai, H.-Z.; Fischer, F. R.; Crommei, M. F.; Rubio, A. “Enediyne Cyclization on Au(111),” J. Amer. Chem. Soc. 2016, 138, 10963–10967, DOI: 10.1021/jacs.6b05203.

InChIs

1: InChI=1S/C22H14/c1-3-9-19(10-4-1)15-17-21-13-7-8-14-22(21)18-16-20-11-5-2-6-12-20/h1-14H
InChIKey=XOJSMLDMLXWRMT-UHFFFAOYSA-N

2: InChI=1S/C22H14/c1-3-9-17(10-4-1)21-15-19-13-7-8-14-20(19)16-22(21)18-11-5-2-6-12-18/h1-14H
InChIKey=DAUFPUDTOKPCMX-UHFFFAOYSA-N

3: InChI=1S/C22H14/c1-3-9-17(10-4-1)15-22-20-14-8-7-13-19(20)16-21(22)18-11-5-2-6-12-18/h1-14H
InChiKey=>FYBPBPGPMCJQNF-UHFFFAOYSA-N

4: InChI=1S/C22H14/c1-3-9-17(10-4-1)20-15-19-13-7-8-14-21(19)22(16-20)18-11-5-2-6-12-18/h1-14H
InChIKey=CYXVOOSYXXUHFV-UHFFFAOYSA-N

5: InChI=1S/C22H14/c1-3-9-17(10-4-1)15-19-16-22(18-11-5-2-6-12-18)21-14-8-7-13-20(19)21/h1-14H
InChIKey=BIKDAEZYYCKGSI-UHFFFAOYSA-N

6: InChI=1S/C22H14/c1-3-9-15(10-4-1)19-17-13-7-8-14-18(17)21-20(22(19)21)16-11-5-2-6-12-16/h1-14H
InChIKey=GAXPSSOZJDJRPN-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Dynamically Complex [6+4] and [4+2] Cycloadditions in the Biosynthesis of Spinosyn A

Patel, A; Chen, Z. Yang, Z; Gutierrez, O.; Liu, H.-W.; Houk, K. N.; Singleton, D. A.  J. Amer. Chem. Soc. 2016,138, 3631-3634
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Enzyme SpnF is implicated in catalyzing the putative [4+2] cycloaddition taking 1 into 3. Houk, Singleton and co-workers have now examined the mechanism of this transformation in aqueous solution but without the enzyme.¹ As might be expected, this mechanism is not straightforward.

Reactant 1, transition states, and products 2 and 3 were optimized at SMD(H2O)/M06-2X/def2-TZVPP//B3LYP-D3(BJ)//6-31+G(d,p). Geometries and relative energies are shown in Figure 1. The reaction1 → 2 is a formal [6+4] cycloaddition, and the reaction 1 → 3 is a formal [4+2] cycloaddition. Interestingly, only a single transition state could be located TS1. It is a bispericyclic TS (see Chapter 4 of my book), where these two pericyclic reaction sort of merge together. After TS1 is traversed the potential energy surface bifurcates, leading to 2 or 3. This is yet again an example of a single TS leading to two different products. (See the many posts I have written on this topic.) The barrier height is 27.6 kcal mol^-1, with 2 lying 13.1 kcal mol^-1 above 3. However, the steepest descent pathway from TS1 leads to 2. There is a second transition state TScope that describes a Cope rearrangement between 2 and 3. Using the more traditional TS theory description, 1 undergoes a [6+4] cycloaddition to form 2 which then crosses a lower barrier (TScope) to form the thermodynamically favored 3, which is the product observed in the enzymatically catalyzed reaction.

1 (0.0)
TS1 (27.6)
2 (4.0)	3 (-9.1)
(24.7)

Figure 1. B3LYP-D3(BJ)//6-31+G(d,p) optimized geometries and relative energies in kcal mol^-1.

Molecular dynamics computations were performed on this system by tracking trajectories starting in the neighborhood of TS1 on a B3LYP-D2/6-31G(d) PES. The results are that 63% of the trajectories end at 2, 25% end at 3, and 12% recross back to reactant 1, suggesting an initial formation ratio for 2:3 of 2.5:1. The reactions are very slow to cross through the “transition zone”, typically 2-3 times longer than for a usual Diels-Alder reaction (see this post).

Once again, we see an example of dynamic effects dictating a reaction mechanism. The authors pose a tantalizing question: Can an enzyme control the outcome of an ambimodal reaction by altering the energy surface such that the steepest downhill path from the transition state leads to the “desired” product(s)? The answer to this question awaits further study.

References

(1) Patel, A; Chen, Z. Yang, Z; Gutierrez, O.; Liu, H.-W.; Houk, K. N.; Singleton, D. A. “Dynamically
Complex [6+4] and [4+2] Cycloadditions in the Biosynthesis of Spinosyn A,” J. Amer. Chem. Soc. 2016,138, 3631-3634, DOI: 10.1021/jacs.6b00017.

InChIs

1: InChI=1S/C24H34O5/c1-3-21-15-12-17-23(27)19(2)22(26)16-10-7-9-14-20(25)13-8-5-4-6-11-18-24(28)29-21/h4-11,16,18-21,23,25,27H,3,12-15,17H2,1-2H3/b6-4+,8-5+,9-7+,16-10+,18-11+/t19-,20+,21-,23-/m0/s1
InChIKey=JEKALMRMHDPSQK-ZTRRSECRSA-N

2: InChI=1S/C24H34O5/c1-3-19-8-6-10-22(26)15(2)23(27)20-12-11-17-14-18(25)13-16(17)7-4-5-9-21(20)24(28)29-19/h4-5,7,9,11-12,15-22,25-26H,3,6,8,10,13-14H2,1-2H3/b7-4-,9-5+,12-11+/t15-,16-,17-,18-,19+,20+,21-,22+/m1/s1
InChIKey=AVLPWIGYFVTVTB-PTACFXJJSA-N

3: InChI=1S/C24H34O5/c1-3-19-5-4-6-22(26)15(2)23(27)11-10-20-16(9-12-24(28)29-19)7-8-17-13-18(25)14-21(17)20/h7-12,15-22,25-26H,3-6,13-14H2,1-2H3/b11-10+,12-9+/t15-,16+,17-,18-,19+,20-,21-,22+/m1/s1
InChIKey=BINMOURRBYQUKD-MBPIVLONSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.