From C60 to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes

Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. J. Am. Chem. Soc. 2016,138, 1420-1429
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

What is the size of a molecule that will stretch computational resources today? Chan and co-workers have examined some very large fullerenes¹ to both answer that question, and also to explore how large a fullerene must be to approach graphene-like properties.

They are interested in predicting the heat of formation of large fullerenes. So, they benchmark the heats of formation of C₆₀ using four different isodesmic reactions (Reaction 1-4), comparing the energies obtained using a variety of different methods and basis sets to those obtained at W1h. The methods include traditional functionals like B3LYP, B3PW91, CAM-B3LYP, PBE1PBE, TPSSh, B98, ωB97X, M06-2X3, and MN12-SX, and supplement them with the D3 dispersion correction. Additionally a number of doubly hybrid methods are tested (again with and without dispersion corrections), such as B2-PLYP, B2GPPLYP, B2K-PLYP, PWP-B95, DSD-PBEPBE, and DSD-B-P86. The cc-pVTZ and cc-pVQZ basis sets were used. Geometries were optimized at B3LYP/6-31G(2df,p).

C60 + 10 benzene → 6 corannulene	Reaction 1
C60 + 10 naphthalene → 8 corannulene	Reaction 2
C60 + 10 phenanthrene → 10 corannulene	Reaction 3
C60 + 10 triphenylene → 12 corannulene	Reaction 4

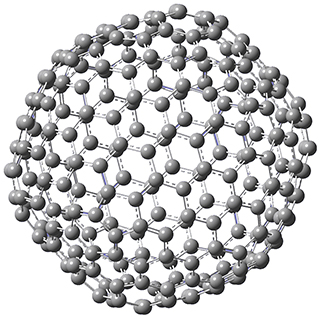
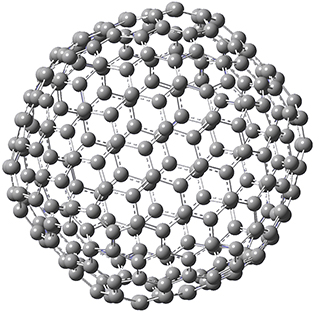
Excellent results were obtained with DSD-PBEPBE-D3/cc-pVQZ (an error of only 1.8 kJ/mol), though even a method like BMK-D3/cc-pVTZ had an error of only 9.2 kJ/mol. They next set out to examine large fullerenes, including such behemoths as C₁₈₀, C₂₄₀, and C₃₂₀, whose geometries are shown in Figure 1. Heats of formation were obtained using isodesmic reactions that compare back to smaller fullerenes, such as in Reaction 5-8.

C70 + 5 styrene → C60 + 5 naphthalene	Reaction 5
C180 → 3 C60	Reaction 6
C320 + 2/3 C60 → 2 C180	Reaction 7

C180

C240

C320

Figure 1. B3LYP/6-31G(2df,p) optimized geometries of C₁₈₀, C₂₄₀, and C₃₂₀. (Don’t forget that clicking on these images will launch Jmol and allow you to manipulate the molecules in real-time.)

Next, taking the heat of formation per C for these fullerenes, using a power law relationship, they were able to extrapolate out the heat of formation per C for truly huge fullerenes, and find the truly massive fullerenes, like C₉₆₈₀, still have heats of formation per carbon 1 kJ/mol greater than for graphene itself.

References

(1) Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. "From C₆₀ to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes," J. Am. Chem. Soc. 2016,138, 1420-1429, DOI: 10.1021/jacs.5b12518.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Theory of Graphene Raman Scattering

Eric J. Heller, Yuan Yang, Lucas Kocia, Wei Chen, Shiang Fang, Mario Borunda, and Efthimios Kaxiras

ACS Nano Article ASAP January 2016 doi:10.1021/acsnano.5b07676

Contributed by Alán Aspuru-Guzik

The recent paper by Eric Heller and collaborators is a tour de force that provides the definitive and correct theory for the unusual features of the Raman spectrum of  perhaps the most popular material of the decade, graphene. Heller and collaborators place in serious doubt literally more than 3000 papers that employ a fourth order perturbative ("double resonance") unphysical model. Instead, the authors employ the Kramers-Heisenberg Dirac model that "has been used ever since to explain more than half a million Raman spectra in a very wide range of systems".

 This paper is also a case study of negative inertia effect in science, where once a dominant theory is established as a de facto explanation, thousands of researchers in a subfield do not examine it further and hence it becomes a dogma. It also shows that unfortunately, cross-pollination of theoretical models and ideas between different communities of scientists can take many years to happen.

Several key elements came into play for this paper. The non-negotiable inclusion of coordinate-dependent transition moments is necessary to reproduce the spectra. In addition, Heller and co-workers introduce a new mechanism, named "transition sliding" that is responsible for the unusual high intensity overtones observed in the spectrum. This transition sliding relies on the linear dispersion and Dirac cones of graphene. The linear dispersion leads to a coherent addition of amplitude in the excited state that reinforces a particular state of graphene (2D). The authors argue that due to the lack of linear dispersion in most if not all other molecules, this effect is mostly absent in regular conjugated polymers due to the lack of constructive interference in such cases.

The article contains a comprehensive discussion of all the other spectral features of the material in a very lucid presentation style.

In summary, the authors make a convincing and irrefutable case for the fact that "[t]here is no reason that removing hydrogens from carbon materials should cause KHD to catastrophically fail and require replacement by a theory based on different physics." This paper should be a must-read for any scholar of two-dimensional materials and a case study for every graduate student of theoretical chemistry.

Atropisomerization of 8-Membered Dibenzolactam: Experimental NMR and Theoretical DFT Study

Buevich, A. V.   J. Org. Chem. 2016, 81, 485–501
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Atropisomers are stereoisomer that differ by axial symmetry, such as in substituted biphenyls or allenes. These acyclic systems have received a fair amount of attention, but now Buevich has looked at atropisomerization that occurs in a ring system.¹ 1 has a biphenyl as part of the eight-member ring, and the biphenyl can exist in either an M or P orientation. Since C3 is chiral (S), the two isomers are (M,S)-1and (P,S)-1. Variable temperature NMR analysis concludes that (P,S)-1 is 1.19 kcal mol^-1 more stable than (M,S)-1, and the barrier for the interchange (P,S)-1 → (M,S)-1 is 26.77 kcal mol^-1.

To identify the process for this atropisomerization process, he utilized B3LYP/6-31G(d) computations of the model system 2. A variety of different techniques were used to identify the local energy minimum conformations of both (M,S)-2 and (P,S)-2, and the lowest energy conformers (M1 for (P,S)-2 and M4 for (M,S)-2) are shown in Figure 1. He then produced a series of 2-D potential energy surfaces varying two of the dihedral angles defining the eight-member ring to help identify potential initial geometries for searching for transition states. (As an aside, this procedure ended up identifying a few additional local energy minima not identified in the initial conformational search – and these all have trans amide groups instead of the cis relationship found initially. These trans isomer are considerably higher in energy than the conformers.) With this model and this computational level, (P,S)-2 is 0.76 kcal mol^-1 lower in energy than (M,S)-2.

M1 0.0	TS1 3.54
M2 2.21	TS4 25.83
M4 0.76

Table 1. B3LYP/6-31G(d) optimized geometries and relative free energies of some critical points along the lowest energy pathway taking (P,S)-2 → (M,S)-2.

A number of transition states were identified, and the lowest energy pathway that takes M1 into M4 first crosses TS1 to make the minimum M2, which than passes a high barrier (25.8 kcal mol^-1) to go to M4. This barrier is in reasonable agreement with the experimental barrier for 1. These TSs are also shown in Figure 1.

Buevich analyzes the conformational process by examination of the changes in the ring dihedral angles following this reaction path. As expected, crossing the highest barrier requires a combination of torsional rotations, but essentially one at a time moving clockwise about the ring.

References

(1) Buevich, A. V. "Atropisomerization of 8-Membered Dibenzolactam: Experimental NMR and Theoretical DFT Study," J. Org. Chem. 2016, 81, 485–501 DOI: 10.1021/acs.joc.5b02321.

InChIs

1: InChI=1S/C27H26N2O/c1-3-12-26-27(30)29(20-21-13-6-5-7-14-21)25-18-11-9-16-23(25)22-15-8-10-17-24(22)28(26)19-4-2/h3-11,13-18,26H,1-2,12,19-20H2/t26-/m0/s1
InChIKey=IYYACMIVKDJSJD-SANMLTNESA-N

2: InChI=1S/C17H18N2O/c1-12-17(20)19(3)16-11-7-5-9-14(16)13-8-4-6-10-15(13)18(12)2/h4-12H,1-3H3/t12-/m0/s1
InChIKey=NIBPKKMKNFOPRM-LBPRGKRZSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Molecular Rift: Virtual Reality for Drug Designers

Magnus Norrby, Christoph Grebner, Joakim Eriksson, and Jonas Boström (2015)
Contributed by Jan Jensen

preview of next version of Molecular Rift now with #Leapmotion sensor attached to the #OculusRift #AugmentedReality pic.twitter.com/5sWmFEsWtS

— Jonas Boström (@DrBostrom) February 5, 2016

The Oculus Rift will be available soon making it one of the first generally available virtual reality headset. There are some molecular visualization programs, like iView, that has an "oculus rift button", but that will "just" make the image on the screen look more three dimensional. While that's great, "head-tracking, allowing the user to look in all directions, and the wide field of view are key components for providing a real VR experience" (see video below).  "Traditional molecular visualizers show molecules in front of you. With Molecular Rift you can step into ligand-protein complexes and feel like you are really there."

An illustration of head-tracking (not Molecular Rift)

Thus, a virtual reality environment for molecular visualization "objects such as atoms and bonds have a location in 3D-space relative to the user’s position" and this is what Molecular Rift provides.  It is written from scratch using the Unity 3D game engine (which only runs on Windows).

Interacting with the image presents an additional challenge since it's hard to interact with a keyboard of mouse while wearing the headset.  To solve this, the authors also interfaced the program with a Microsoft Kinect.  The code is open source and available on GitHub.

While Molecular Rift is primarily meant for drug design, the Molecular Rift would also clearly be fantastic for teaching, especially if a smartphone version (minus the Kinect interface) could be made to be used in conjunction with Google Cardboard.

Another fantastic extension would be an interface with Reiher's Interactive Chemical Reactivity Exploration tool.




This work is licensed under a Creative Commons Attribution 4.0

QM/MM Protocol for Direct Molecular Dynamics of Chemical Reactions in Solution: The Water-Accelerated Diels–Alder Reaction

Yang, Z.; Doubleday, C.; Houk, K. N. J. Chem. Theor. Comput. 2015,  5606-5612
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

I discuss the aqueous Diels-Alder reaction in Chapter 7.1 of my book. A key case is the reaction of methyl vinyl ketone with cyclopentadiene, Reaction 1. The reaction is accelerated by a factor of 740 in water over the rate in isooctane.¹ Jorgensen argues that this acceleration is due to stronger hydrogen bonding to the ketone than in the transition state than in the reactants.^2-4

Rxn 1

Doubleday and Houk⁵ report a procedure for calculating trajectories including explicit water as the solvent and apply it to Reaction 1. Their process is as follows:

1. Compute the endo TS at M06-2X/6-31G(d) with a continuum solvent.
2. Equilibrate water for 200ps, defined by the TIP3P model, in a periodic box, with the transition state frozen.
3. Continue the equilibration as in Step 2, and save the coordinates of the water molecules after every addition 5 ps, for a total of typically 25 steps.
4. For each of these solvent configurations, perform an ONIOM computation, keeping the waters fixed and finding a new optimum TS. Call these solvent-perturbed transition states (SPTS).
5. Generate about 10 initial conditions using quasiclassical TS mode sampling for each SPTS.
6. Now for each the initial conditions for each of these SPTSs, run the trajectories in the forward and backward directions, typically about 10 of them, using ONIOM to compute energies and gradients.
7. A few SPTS are also selected and water molecules that are either directly hydrogen bonded to the ketone, or one neighbor away are also included in the QM portion of the ONIOM, and trajectories computed for these select sets.

The trajectory computations confirm the role of hydrogen bonding in stabilizing the TS preferentially over the reactants. Additionally, the trajectories show an increasing asynchronous reactions as the number of explicit water molecules are included in the QM part of the calculation. Despite an increasing time gap between the formation of the first and second C-C bonds, the overwhelming majority of the trajectories indicate a concerted reaction.

References

(1) Breslow, R.; Guo, T. "Diels-Alder reactions in nonaqueous polar solvents. Kinetic
effects of chaotropic and antichaotropic agents and of β-cyclodextrin," J. Am. Chem. Soc. 1988, 110, 5613-5617, DOI: 10.1021/ja00225a003.

(2) Blake, J. F.; Lim, D.; Jorgensen, W. L. "Enhanced Hydrogen Bonding of Water to Diels-Alder Transition States. Ab Initio Evidence," J. Org. Chem. 1994, 59, 803-805, DOI: 10.1021/jo00083a021.

(3) Chandrasekhar, J.; Shariffskul, S.; Jorgensen, W. L. "QM/MM Simulations for Diels-Alder
Reactions in Water: Contribution of Enhanced Hydrogen Bonding at the Transition State to the Solvent Effect," J. Phys. Chem. B 2002, 106, 8078-8085, DOI: 10.1021/jp020326p.

(4) Acevedo, O.; Jorgensen, W. L. "Understanding Rate Accelerations for Diels−Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theor. Comput. 2007, 3, 1412-1419, DOI:10.1021/ct700078b.

(5) Yang, Z.; Doubleday, C.; Houk, K. N. "QM/MM Protocol for Direct Molecular Dynamics of Chemical Reactions in Solution: The Water-Accelerated Diels–Alder Reaction," J. Chem. Theor. Comput. 2015, , 5606-5612, DOI: 10.1021/acs.jctc.5b01029.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.