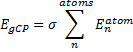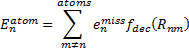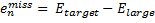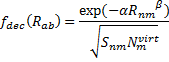Xia, J.; Golder, M. R.; Foster, M. E.; Wong, B. M.; Jasti, R. J. Am. Chem. Soc. 2012, 134, 19709
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
Nanotubes are currently constructed in ways that offer little control of their size and chirality. The recent synthesis of cycloparaphenylenes (CPP) provides some hope that fully controlled synthesis of nanotubes might be possible in the near future. Jasti has now made an important step forward in preparing dimers of CPP such as 1.1
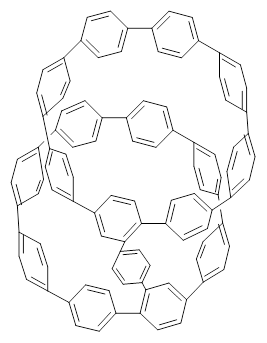 1 |  2 |
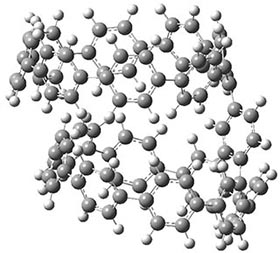
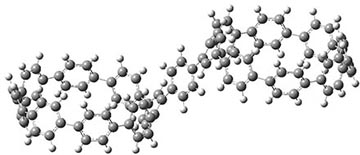
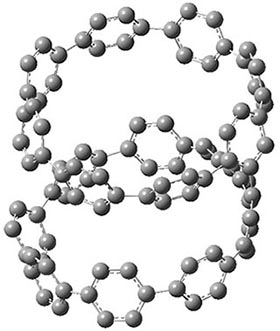
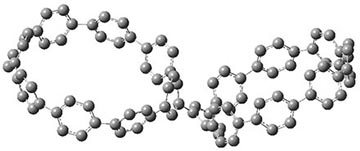
They also performed B3LYP-D/6-31G(d,p) computations on 1 and the directly linked dimer 2. The optimized geometries of these two compounds in their cis and trans conformations are shown in Figure 1. Interestingly, both compounds prefer to be in the cis conformation; cis-1 is 10 kcal mol-1 more stable than trans-1 and cis-2 is 30 kcal mol-1 more stable than the trans isomer. While a true transition state interconnecting the two isomers was not located, a series of constrained optimizations to map out a reaction surface suggests that the barrier for 1 is about 13 kcal mol-1. The authors supply an interesting movie of this pseudo-reaction path (download the movie).
cis-1
|
trans-1
|
cis-2
|
trans-2
|
Figure 1. B3LYP-D/6-31G(d,p) optimized geometries of the cis and trans conformers of 1 and 2. (Be sure to click on these images to launch a 3-D viewer; these structures come to life in 3-D!)
References
(1) Xia, J.; Golder, M. R.; Foster, M. E.; Wong, B. M.; Jasti, R. "Synthesis, Characterization, and Computational Studies of Cycloparaphenylene Dimers," J. Am. Chem. Soc. 2012, 134, 19709-19715, DOI: 10.1021/ja307373r.
InChIs
1: InChI=1S/C106H82/c1-5-13-79-21-9-17-76-29-37-85(38-30-76)95-59-63-98(64-60-95)103-71-69-101(82(16-8-4)24-12-20-77-27-35-84(36-28-77)90-51-55-94(56-52-90)91-45-41-86(79)42-46-91)73-105(103)99-65-67-100(68-66-99)106-74-102-70-72-104(106)97-61-57-88(58-62-97)81(15-7-3)23-10-18-75-25-33-83(34-26-75)89-49-53-93(54-50-89)92-47-43-87(44-48-92)80(14-6-2)22-11-19-78-31-39-96(102)40-32-78/h5-16,21-74H,1-4,17-20H2/b21-9-,22-11-,23-10-,24-12-,79-13+,80-14+,81-15+,82-16+
InChIKey=WFVBBCVHFBTQRK-VPGVYKRGSA-N
InChIKey=WFVBBCVHFBTQRK-VPGVYKRGSA-N
2: InChI=1S/C100H78/c1-5-13-75-21-9-17-72-29-37-81(38-30-72)91-59-63-94(64-60-91)97-67-65-95(78(16-8-4)24-12-20-73-27-35-80(36-28-73)86-51-55-90(56-52-86)87-45-41-82(75)42-46-87)69-99(97)100-70-96-66-68-98(100)93-61-57-84(58-62-93)77(15-7-3)23-10-18-71-25-33-79(34-26-71)85-49-53-89(54-50-85)88-47-43-83(44-48-88)76(14-6-2)22-11-19-74-31-39-92(96)40-32-74/h5-16,21-70H,1-4,17-20H2/b21-9-,22-11-,23-10-,24-12-,75-13+,76-14+,77-15+,78-16+
InChIKey=HOODCSIDKUJYKE-XJQPCHFNSA-N
InChIKey=HOODCSIDKUJYKE-XJQPCHFNSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.