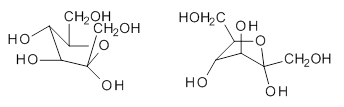
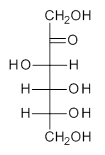
Jacobsen, R. L.; Johnson, R. D.; Irikura, K. K.; Kacker, R. N. J. Chem. Theor. Comput. 2013, 9, 951
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
Vibrational frequencies are routinely computed within most QM codes assuming the harmonic approximation. To correct for the neglect of higher order terms (anharmonicity), along with correcting for the inherent approximations of whatever quantum mechanical method is used, the harmonic frequencies are typically corrected by using a multiplicative scaling factor. The values of the scaling factor is method-dependent: a different scaling factor is need for every method and basis set combination! Nonetheless, this is a simple approach to computing often quite reasonable vibrational frequencies.
Anharmonic corrections can also be computed, and this is usually done using perturbation theory, which requires computing the third and often fourth derivatives, a mightily expensive proposition for reasonably large molecules even with DFT, let alone with some wavefunction-based post-HF method.
Jacobsen and co-workers1 examined a set of 176 molecules that include 2738 vibrational modes, using HF, MP2, B3LYP and PBE0 with the 6-31G(d) or 6-31+G(d,p) basis sets. The unscaled anharmonic frequencies are much better than the unscaled harmonic frequencies; for example, using B3LYP/6-31+G(d), the root mean square deviation (RMSD) for the harmonic frequencies is 78 cm-1 and 36 cm-1for the anharmonic frequencies. But the scaled harmonic frequencies are just as good as the scaled anharmonic frequencies; using the same QM method, the RMSD for the scaled harmonic frequencies is 38 cm-1 and 36 cm-1 for the scaled anharmonic frequencies.
These authors suggest that accurate anharmonic corrections require very accurate potential energy surfaces, and so they recommend that unless you are using a very highly accurate computational model, there is no point in computing anharmonic frequencies; scaled harmonic frequencies will suffice!
References
(1) Jacobsen, R. L.; Johnson, R. D.; Irikura, K. K.; Kacker, R. N. "Anharmonic Vibrational Frequency Calculations Are Not Worthwhile for Small Basis Sets," J. Chem. Theor. Comput. 2013, 9, 951-954, DOI:10.1021/ct300293a.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.