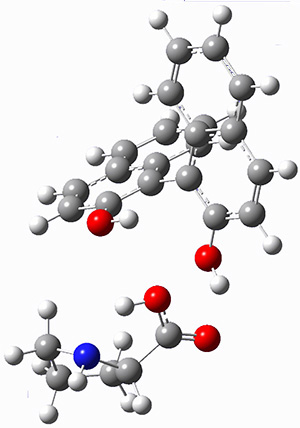
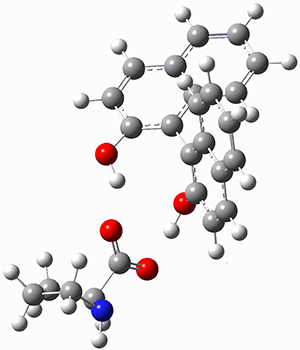
Mariana Rossi, Sucismita Chutia, Matthias Scheffler, and Volker Blum J. Phys. Chem. A 2014 ASAP
Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission
Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission
Weak interactions are difficult to model in general; there are some DFT functional which do a reasonable job on hydrogen bonding (e.g. PBE[1,2]), and there have been a number of interesting developments in the modelling of van der Waals (dispersion) forces, which I will write about in future.
A recent paper in J. Phys. Chem A by Rossi et al. (available on-line[3] and part of an on-going series of studies on peptides in DFT) gives an excellent discussion of one avenue of work pushing towards accuracy for weak bonds. The approach used for dispersion is efficient and promising (the TS vdW[4] and MBD[5] method), but there are still questions that remain.
The paper uses DFT and enhancements (hybrid functionals and dispersion corrections) to study a large peptide with around 100 atoms, for which there is excellent experimental information available[6] (in particular, the data is from the gas phase, which DFT can easily compare to). They use the FHI-aims code[7], which is a relatively new all-electron code with numerical atomic orbitals as a basis set. An important question that must be asked about this type of basis concerns basis-set superposition error (an error in energy normally found when comparing fragments of a system to the complete system, but which will have some effect when comparing compact conformers to sparse conformers). This is not discussed in the paper, though previous work has shown that for the higher accuracy basis used (tier-2) BSSE is not a dominant error; moreover, BSSE within a molecule will be a smaller effect than between molecules.
A previous study of the peptide fragment[8] found that 17 different GGAs failed to reproduce the experimental ordering of the four lowest energy conformers; Rossi et al find that hybrid functionals, dispersion and vibrational effects are needed to get this correct. However, Rossi et al. find that hybrid DFT with dispersion finds the right family of structures to be lowest in energy.
There are a number of questions that are raised by the study:
- What would the effect of a different hybrid functional be ?
- What would the effect of a different dispersion scheme be ?
- Are the vibrational data accurate enough ? (They were calculated with PBE and vdW – no hybrid functional and the less accurate dispersion approach; the authors acknowledge the difficulty of vibrational calculations, and did do one with PBE0+vdW though it gave no better agreement with experiment)
There are many different hybrid functionals available, most of which are parameterised for specific purposes (be that a specific system or to fit specific limits). As the most expensive part of the calculations done by Rossi et al. is the exchange (as is often the case) it is reasonable that they have not tested this extensively, but they do note that changing to HSE06 changes the energies between helical and non-helical conformers by ~20meV (compared to energy differences between families of 50-100meV, so it’s not insignificant).
I would be most interested to see the effect of the vdW-DF functionals[9] (I should note that I collaborated on a widely-cited study of the effects of tuning the exchange functional used with the vdW-DF functional[10]). These functionals take a completely different approach to dispersion to the TS approach (or the Grimme DFT-D approach) and would give an important view on the effects of dispersion.
It’s really good to see studies like these, pushing forward the accuracy that can be achieved by DFT, testing weak interactions, and being honest about how effective different methods are. But there is still more work to be done.
[1] J. Phys. Chem. A 108, 5692 (2004) 10.1021/jp0377073
[2] J. Phys.: Condens. Matter 20 294201 (2008) 10.1088/0953-8984/20/29/294201
[3] J. Phys. Chem. A (2014) 10.1021/jp412055r
[4] Phys. Rev. Lett. 102, 073005 (2009) 10.1103/PhysRevLett.102.073005
[5] Phys. Rev. Lett. 108, 236402 (2012) 10.1103/PhysRevLett.108.236402
[6] J. Am. Chem. Soc. 129, 13820 (2007) 10.1021/ja076507s
[7] Comp. Phys. Commun. 180, 2175 (2009) 10.1016/j.cpc.2009.06.022
[8] Chem. Eur. J 18, 12941 (2012) 10.1002/chem.201202068
[9] Phys. Rev. Lett. 92, 246401 (2004) 10.1103/PhysRevLett.92.246401
[10] J. Phys.: Condens. Matter 22 022201 (2010) 10.1088/0953-8984/22/2/022201
[2] J. Phys.: Condens. Matter 20 294201 (2008) 10.1088/0953-8984/20/29/294201
[3] J. Phys. Chem. A (2014) 10.1021/jp412055r
[4] Phys. Rev. Lett. 102, 073005 (2009) 10.1103/PhysRevLett.102.073005
[5] Phys. Rev. Lett. 108, 236402 (2012) 10.1103/PhysRevLett.108.236402
[6] J. Am. Chem. Soc. 129, 13820 (2007) 10.1021/ja076507s
[7] Comp. Phys. Commun. 180, 2175 (2009) 10.1016/j.cpc.2009.06.022
[8] Chem. Eur. J 18, 12941 (2012) 10.1002/chem.201202068
[9] Phys. Rev. Lett. 92, 246401 (2004) 10.1103/PhysRevLett.92.246401
[10] J. Phys.: Condens. Matter 22 022201 (2010) 10.1088/0953-8984/22/2/022201