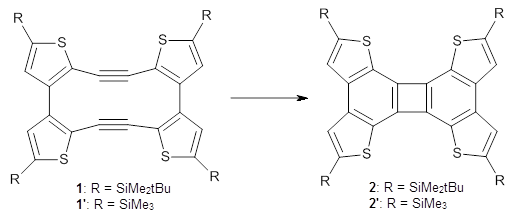
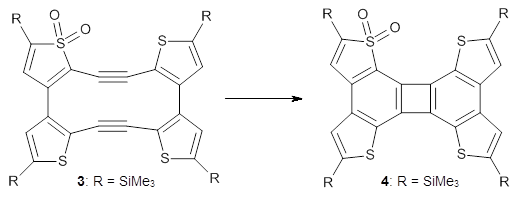
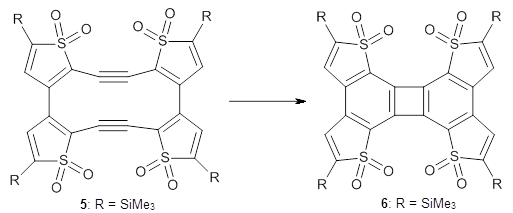
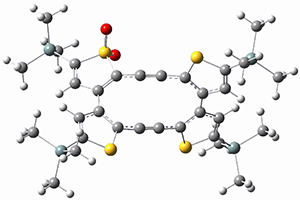
Debora S. Marks, Thomas A. Hopf and Chris Sander Nature Biotechnology 2012, 30, 1072
Contributed by +Jan Jensen
This perspective paper gives a great overview of a very new and very promising sub-field of computational protein structure determination that started with this 2011 paper (see also this interesting blogpost). The method predicts distance restraints between two amino acids by looking for correlated changes in the protein sequence. These distance restraints are then used to determine 3D protein structures using the same software package used to compute NMR structures using NOE constraints.
The method has been tested on globular and membrane proteins up to 258 and 483 amino acids, respectively. About 0.5 to 0.75 predicted constraints per residue is needed and ca 5$L$ (where $L$ is the number of amino acids) diverse sequences are needed to produce reasonable protein structures with $C_\alpha$ RMSDs < 5 Å relative to the corresponding x-ray structures.
A $C_\alpha$ RMSD of 5 Å may sounds like a lot but active site geometries may be significantly more accurate due to "strong evolutionary constraints". For example while the structure of trypsin was predicted with a $C_\alpha$ RMSD of 4.3 Å, the relative orientation of the catalytic triad was predicted with a $C_\alpha$ RMSD of only 0.6 Å (1.3 Å all atom-RMSD).
Furthermore, x-ray structures are often refined using, for example, MD simulations before they are used in computational studies. I would be very interesting to compare computational predictions (e.g. activation energies, pKa values of active site residues, or docking scores) based on x-ray structures and evolutionary constraints, i.e. to compare their chemical accuracy.
The number of available sequences is growing very quickly, so I believe the main general issue that must be addressed with this method is the efficient prediction of structures of globular proteins larger than ca 400 amino acids using distance restraints. This is still quite a demanding task.
The authors provide a very nice web-service for the prediction of contacts and structures, which I have used in my own research.
In conclusion, this method provides a very nice complement to homology modeling for cases where no close structural homologs, but many sequence homologues, are available. Given the pace with which new sequences are determined it won't be too many years before a reasonable protein structure can be predicted for the vast majority of cases.

This work is licensed under a Creative Commons Attribution 4.0 International License.
Contributed by +Jan Jensen
The method has been tested on globular and membrane proteins up to 258 and 483 amino acids, respectively. About 0.5 to 0.75 predicted constraints per residue is needed and ca 5$L$ (where $L$ is the number of amino acids) diverse sequences are needed to produce reasonable protein structures with $C_\alpha$ RMSDs < 5 Å relative to the corresponding x-ray structures.
A $C_\alpha$ RMSD of 5 Å may sounds like a lot but active site geometries may be significantly more accurate due to "strong evolutionary constraints". For example while the structure of trypsin was predicted with a $C_\alpha$ RMSD of 4.3 Å, the relative orientation of the catalytic triad was predicted with a $C_\alpha$ RMSD of only 0.6 Å (1.3 Å all atom-RMSD).
Furthermore, x-ray structures are often refined using, for example, MD simulations before they are used in computational studies. I would be very interesting to compare computational predictions (e.g. activation energies, pKa values of active site residues, or docking scores) based on x-ray structures and evolutionary constraints, i.e. to compare their chemical accuracy.
The number of available sequences is growing very quickly, so I believe the main general issue that must be addressed with this method is the efficient prediction of structures of globular proteins larger than ca 400 amino acids using distance restraints. This is still quite a demanding task.
The authors provide a very nice web-service for the prediction of contacts and structures, which I have used in my own research.
In conclusion, this method provides a very nice complement to homology modeling for cases where no close structural homologs, but many sequence homologues, are available. Given the pace with which new sequences are determined it won't be too many years before a reasonable protein structure can be predicted for the vast majority of cases.

This work is licensed under a Creative Commons Attribution 4.0 International License.