Kurt Lejaeghere, Gustav Bihlmayer, Torbjörn Björkman, Peter Blaha, Stefan Blügel,Volker Blum, Damien Caliste, Ivano E. Castelli, Stewart J. Clark, Andrea Dal Corso,Stefano de Gironcoli, Thierry Deutsch, John Kay Dewhurst, Igor Di Marco, Claudia Draxl,Marcin Dułak, Olle Eriksson, José A. Flores-Livas, Kevin F. Garrity, Luigi Genovese,Paolo Giannozzi, Matteo Giantomassi, Stefan Goedecker, Xavier Gonze, Oscar Grånäs,E. K. U. Gross, Andris Gulans, François Gygi, D. R. Hamann, Phil J. Hasnip,N. A. W. Holzwarth, Diana Ius¸an, Dominik B. Jochym, François Jollet, Daniel Jones,Georg Kresse, Klaus Koepernik, Emine Küçükbenli, Yaroslav O. Kvashnin,Inka L. M. Locht, Sven Lubeck, Martijn Marsman, Nicola Marzari, Ulrike Nitzsche,Lars Nordström, Taisuke Ozaki, Lorenzo Paulatto, Chris J. Pickard, Ward Poelmans,Matt I. J. Probert, Keith Refson, Manuel Richter, Gian-Marco Rignanese, Santanu Saha,Matthias Scheffler, Martin Schlipf, Karlheinz Schwarz, Sangeeta Sharma,Francesca Tavazza, Patrik Thunström, Alexandre Tkatchenko, Marc Torrent,David Vanderbilt, Michiel J. van Setten, Veronique Van Speybroeck, John M. Wills,Jonathan R. Yates, Guo-Xu Zhang, Stefaan Cottenier Science 2016, 351, aad3000
Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission
Reposted from Atomistic Computer Simulations with permission
A paper in Science (or equivalent journal) generally reports novel or ground-breaking research. At first sight, the paper I’ll discuss in this post[1] does not fit into that category: it reports an extensive set of tests on calculations for the equation of state (EOS) for 71 elemental solids using a variety of DFT codes, all using the PBE functional.
This paper is the product of a collaboration (you can find all the data, test suites etc on their web site[2]) that has been going for a while, and is both important and impressive. They have defined a single parameter, delta, which allows them to compare EOS calculated with different codes, giving a simple route to evaluating the reproducibility of DFT. This is immensely valuable, because different codes use different basis sets, different numerical solvers and different approaches to the external potential (full potential or a variety of pseudopotentials), and as a result will give different answers for the same simulation. The question is: how different are the answers ?
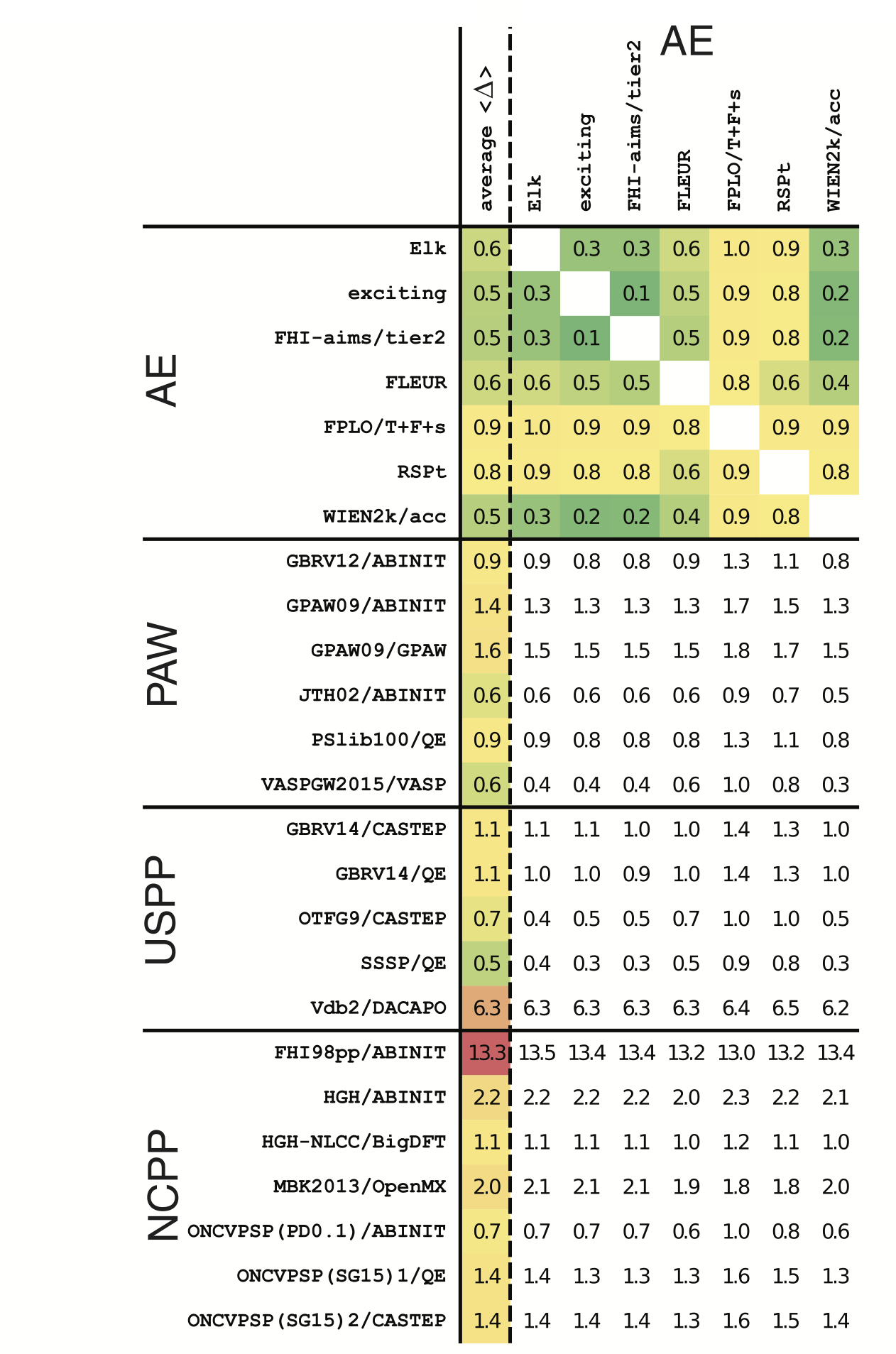
The key result from this paper is that modern DFT codes now achieve a precision[3] which is better than experimental; in terms of the paper, this means a delta value which is better than 1 meV/atom. This precision applies across various basis sets: plane waves, augmented plane waves, and numerical orbitals. It also applies to all-electron, PAW, and both ultra-soft and norm-conserving pseudopotential calculations. The summary table from the paper is reproduced below; the numbers given are the RMS value for delta across all 71 elements, while the colour indicates overall reliability.

Why is this work significant ? First, it gives a way to test new DFT codes and implementations, basis sets and approaches to the potential. So we now have an absolute reference against which codes can be compared. Second, it shows that there are now freely-available pseudopotential libraries which are precise in comparison to all-electron results (this is something that wasn’t true even five years ago - their Table 2, which shows the changing precision of different libraries over time, is fascinating). For both users and code developers, this is great news: there is no longer any question as to whether a particular pseudopotential is reliable, certainly within the context of single elements.
What could be added to the study ? Here are some ideas:
- More extensive tests. There are no tests of elements in different environments - and this can pose extreme challenges to pseudopotentials (think of the different oxidation states of transition metals, for instance).
- A comparison between the codes (e.g. speed, memory or parallelisation).
This would be very challenging, but would be interesting data. - More functionals and extensions of DFT will be important to include.
This paper is an immensely valuable contribution to the electronic structure community, as well as the wider scientific community, and it is good to see it published in a high-profile journal.
[3] Precision indicates the spread between different measured values, while accuracy indicates the deviation from the correct result (however “correct” is defined !)
No comments:
Post a Comment