Justin S. Smith, Olexandr Isayev, Adrian E. Roitberg (2016)
Contributed by Jan Jensen
This paper basically presents a neural network force field, which the authors call a neural network potential (NNP). The authors heavily modify the Behler-Parinello symmetry functions (also used in this CCH) to improve the transferability and train it against 13.8 million ωB97X/6-31G(d) energies computed for CHON-containing molecules with 8 or less non-hydrogen atoms. This huge training set made it possible to parameterise a neural net with three hidden layers with a total of 320 nodes and 124,033 optimisable parameters. Deep learning indeed.
Contributed by Jan Jensen
This paper basically presents a neural network force field, which the authors call a neural network potential (NNP). The authors heavily modify the Behler-Parinello symmetry functions (also used in this CCH) to improve the transferability and train it against 13.8 million ωB97X/6-31G(d) energies computed for CHON-containing molecules with 8 or less non-hydrogen atoms. This huge training set made it possible to parameterise a neural net with three hidden layers with a total of 320 nodes and 124,033 optimisable parameters. Deep learning indeed.
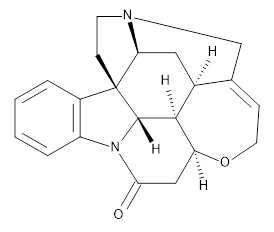
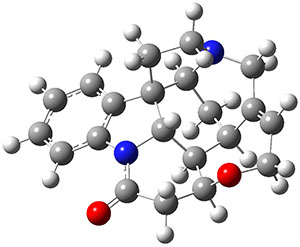
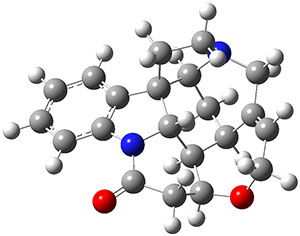
What makes this work particularly exiting is that the NNP appears to be transferable to larger molecules. For example, the figure above shows that the NNP can reproduce the relative ωB97X/6-31G(d) energies of retinol conformers with en RMSE of 0.6 kcal/mol. For comparison the corresponding value for DFTB (not clear if it's DFTB2 or DFTB3) is 1.2 kcal/mol, although ωB97X/6-31G(d) is not the definitive reference by which to judge DFTB accuracy.
I think this work holds a lot of promise. One of the key challenges is to reduce the size of the training set to a point where high level calculations can be used to compute the energies. Alternatively, perhaps approaches like ∆-machine learning can be used to correct the NNP using a smaller representative training set.