Grimme, S.; Steinmetz, M. Phys. Chem. Chem. Phys. 2013, 15, 16031
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Reposted from Computational Organic Chemistry with permission
The importance of dispersion in determining molecular structure, even the structure of a single medium-sized molecule, is now well recognized. This means that quantum methods that do not account for dispersion might give very poor structures.
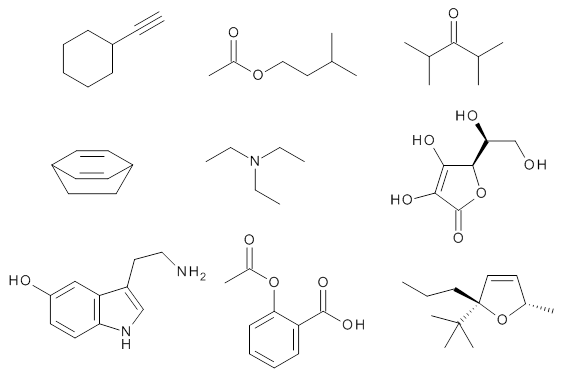
Grimme1 takes an interesting new twist towards assessing the geometries produced by computational methods by evaluating the structures based on their rotational constants B0 obtained from microwave experiments. He uses nine different molecules in his test set, shown in Scheme 1. This yields 25 different rotational constants (only one rotational constant is available from the experiment on triethylamine). He evaluates a number of different computational methods, particularly DFT with and without a dispersion correction (either the D3 or the non-local correction). The fully optimized geometry of each compound with each method is located to then the rotational constants are computed. Since this provides Be values, he has computed the vibrational correction to each rotational constant for each molecule, in order to get “experimental” Be values for comparisons.
Scheme 1.

Grimme first examines the basis set effect for vitamin C and aspirin using B3LYP-D3. He concludes that def2-TZVP or lager basis sets are necessary for reliable structures. However, the errors in the rotational constant obtained at B3LYP-D3/6-31G* is at most 1.7%, and even with CBS the error can be as large as 1.1%, so to my eye even this very small basis set may be completely adequate for many purposes.
In terms of the different functionals (using the DZVP basis set), the best results are obtained with the double hybrid B2PLYP-D3 functional where the mean relative deviation is only 0.3%; omitting the dispersion correction only increases the mean error to 0.6%. Common functionals lacking the dispersion correction have mean errors of about 2-3%, but with the correction, the error is appreciably diminished. In fact B3LYP-D3 has a mean error of 0.9% and B3LYP-NL has an error of only 0.6%. In general, the performance follows the Jacob’s Ladder hierarchy.
References
(1) Grimme, S.; Steinmetz, M. "Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase," Phys. Chem. Chem. Phys. 2013, 15, 16031-16042, DOI: 10.1039/C3CP52293H.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
No comments:
Post a Comment