Pérez-Estrada, S.; Rodrı́guez-Molina, B.; Xiao, L.; Santillan, R.; Jiménez-Osés, G.; Houk, K. N.; Garcia-Garibay, M. A. J. Am. Chem. Soc. 2015, 137, 2175
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
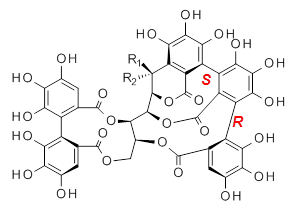
Molecular rotors remain a fascinating topic – the idea of creating a miniature motor just seems to capture the imagination of scientists. Garcia-Garibay and his group have synthesized the interesting rotor 1, and in collaboration with the Houk group, they have utilized computations to help understand the dynamics of this rotor.1
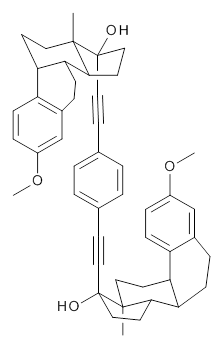 1 |
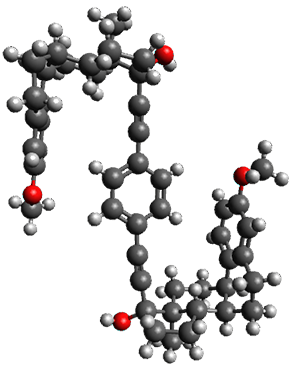
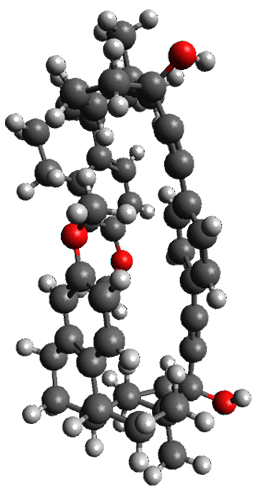
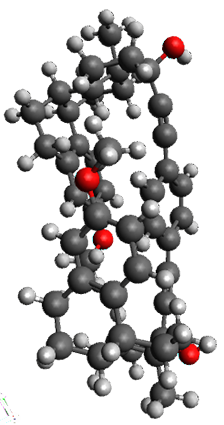
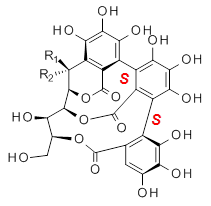
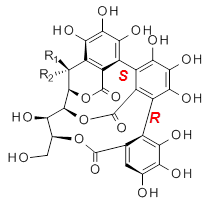
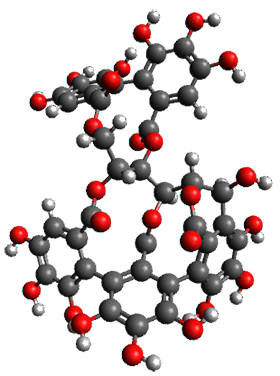
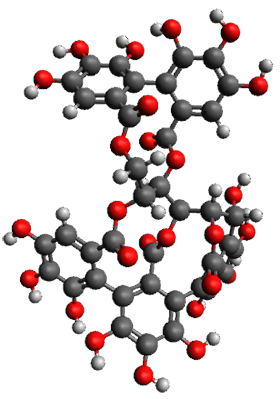
The x-ray structure of this compound, shown in Figure 1, displays two close interactions of a hydrogen on the central phenyl ring with the face of one of the steroidal phenyl rings. Rotation of the central phenyl ring is expected to then “turn off” one or both of these C-H…π interactions. The authors argue this as a competition between the molecule sampling an enthalpic region, where the molecule has one or two favorable C-H…π interactions, and the large entropic region where these C-H…π interactions do not occur, but this space is expected to have a large quantity of energetically similar conformations.
x-ray
| |
1a
|
1b
|
Figure 1. X-ray and M06-2x/6-31G(d) optimized structures of 1.
Variable temperature NMR finds the central phenyl hydrogen with a chemical shift of 6.55ppm at 295 K but at 6.32 ppm at 222 K. This suggest as freezing of the conformations at low temperature favoring those conformations possessing the internal C-H…π interactions. M06-2X/6-31G(d) optimization finds two low-energy conformations with a single C-H…π interaction. These are shown in Figure 1. No competing conformation was found to have two such interactions. Computations of the chemical shifts of these conformations show the upfield shift of the central phenyl hydrogens. Fitting these chemical shifts to the temperature data gives ΔH = -1.74 kcal mol-1, ΔS = -5.12 esu and ΔG = -0.21 kcal mol-1 for the enthalpic region to entropic region transition.
References
(1) Pérez-Estrada, S.; Rodrı́guez-Molina, B.; Xiao, L.; Santillan, R.; Jiménez-Osés, G.; Houk, K. N.; Garcia-Garibay, M. A. "Thermodynamic Evaluation of Aromatic CH/π Interactions and Rotational Entropy in a Molecular Rotor," J. Am. Chem. Soc. 2015, 137, 2175-2178, DOI: 10.1021/ja512053t.
InChIs
1: InChI=1S/C48H54O4/c1-45-23-19-39-37-15-11-35(51-3)29-33(37)9-13-41(39)43(45)21-27-47(45,49)25-17-31-5-7-32(8-6-31)18-26-48(50)28-22-44-42-14-10-34-30-36(52-4)12-16-38(34)40(42)20-24-46(44,48)2/h5-8,11-12,15-16,29-30,39-44,49-50H,9-10,13-14,19-24,27-28H2,1-4H3
InChIKey=CXZHCTLIHKZRMW-UHFFFAOYSA-N
InChIKey=CXZHCTLIHKZRMW-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.