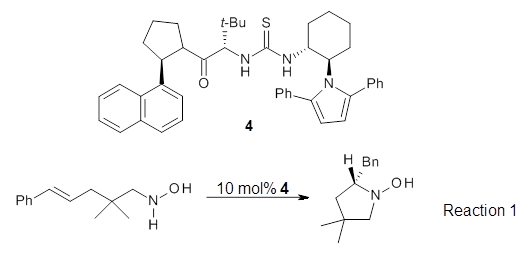
Stefan Grimme Angew. Chem. Int. Ed. 2013, 52, 6306
Contributed by +Jan Jensen
Quantum chemistry has contributed significantly to nearly all spectroscopic methods used in chemistry, but comparatively less so for mass spectrometry. This might be about to change thanks to this very interesting study by Stefan Grimme.
Grimme presents a new program called QCEIMS, which together with the quantum programs ORCA, DFTB+, and MNDO, is used to predict electron impact mass spectra of molecules in a black box fashion.
The method starts with a ca 50 ps equilibrated ground state NVE Born-Oppenheimer MD simulation of the neutral molecule (M) using, for example, OM2 or DFTB3 (typically at 500 K).
The ionization from electron impact is simulated by randomly choosing a number of snapshots as starting points for new 5-10 ps NVE MD simulations with excess thermal energy. Unrestricted, fractional occupation number wavefunctions are used and excess thermal energy is applied at the first step of each MD. OM2 or DFTB3 can usually be used but KS-DFT/DZ may be necessary for cases where the fragmentations involve complex reaction mechanisms.
The charged fragments in the resulting "hot ion" ensemble are then identified and counted to yield the mass spectrum. Roughly 1-100 million energy and gradient evaluations are needed for good agreement with experimental spectra.

This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Contributed by +Jan Jensen
Quantum chemistry has contributed significantly to nearly all spectroscopic methods used in chemistry, but comparatively less so for mass spectrometry. This might be about to change thanks to this very interesting study by Stefan Grimme.
Grimme presents a new program called QCEIMS, which together with the quantum programs ORCA, DFTB+, and MNDO, is used to predict electron impact mass spectra of molecules in a black box fashion.
The method starts with a ca 50 ps equilibrated ground state NVE Born-Oppenheimer MD simulation of the neutral molecule (M) using, for example, OM2 or DFTB3 (typically at 500 K).
The ionization from electron impact is simulated by randomly choosing a number of snapshots as starting points for new 5-10 ps NVE MD simulations with excess thermal energy. Unrestricted, fractional occupation number wavefunctions are used and excess thermal energy is applied at the first step of each MD. OM2 or DFTB3 can usually be used but KS-DFT/DZ may be necessary for cases where the fragmentations involve complex reaction mechanisms.
The charged fragments in the resulting "hot ion" ensemble are then identified and counted to yield the mass spectrum. Roughly 1-100 million energy and gradient evaluations are needed for good agreement with experimental spectra.

This work is licensed under a Creative Commons Attribution 3.0 Unported License.