Hypercubane: DFT-based prediction of an Oh-symmetric double-shell hydrocarbon

Pichierri, F. Chem. Phys. Lett. 2014, 612, 198-202
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

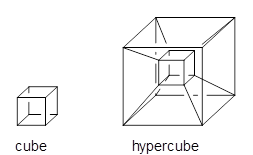
Three-dimensional objects can be projected into four-dimensional objects. So for example a cube can be projected into a hypercube, as in Scheme 1.

Scheme 1.

Pichierri proposes a hydrocarbon analogue of the hypercube. The critical decision is the connecting bridge between the outer (exploded) carbons. This distance is too long to be a single carbon-carbon bond. Pichierri opts to use ethynyl bridges, to give the hypercube 1.¹

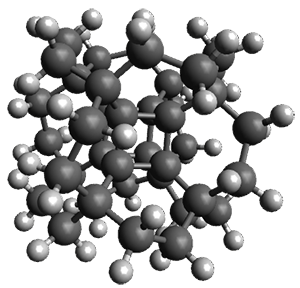
Now, unfortunately he does not supply any supporting materials. So I have reoptimized this O_h geometry at B3LYP/6-31G(d), and show this structure in Figure 1. Pichierri does not report much beyond the geometry of 1 and the perfluoronated analogue. One interesting property that might be of interest is the ring strain energy of 1, which I will not take up here.

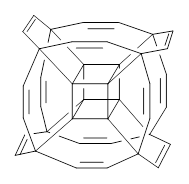1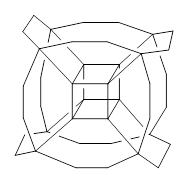

2

But a question I will take up is just what bridges might serve to create the hydrocarbon hypercube. A more fundamental choice might be ethanyl bridges, to create 2. However, the O_h conformer of 2 has 13 imaginary frequencies at B3LYP/6-31G(d). Lowering the symmetry to D₃ give a structure that has only real frequencies, and it’s shown in Figure 1. An interesting exercise is to ponder other choices of bridges, which I will leave for the reader.

1

2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2.
As always, be sure to click on the image to enable Jmol for interactive viewing of these interesting structures!

References

(1) Pichierri, F. "Hypercubane: DFT-based prediction of an O_h-symmetric double-shell hydrocarbon,"Chem. Phys. Lett. 2014, 612, 198-202, DOI: j.cplett.2014.08.032.

InChIs

1: InChI=1S/C40H24/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H
InChIKey=FFMFUIDOGFAUOP-UHFFFAOYSA-N

2: InChI=1S/C40H48/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H2
InChIKey=MCSZKKKJCDSRIV-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.